
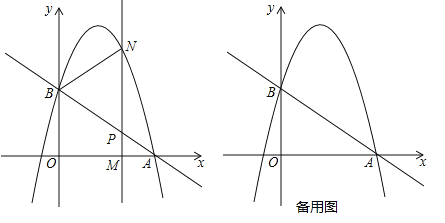
【题目】如图,抛物线![]() 过点
过点![]() 和
和![]() ,点
,点![]() 为线段
为线段![]() 上一个动点(点
上一个动点(点![]() 与点
与点![]() 不重合),过点
不重合),过点![]() 作垂直于
作垂直于![]() 轴的直线与直线
轴的直线与直线![]() 和抛物线分别交于点
和抛物线分别交于点![]() .
.
(1)求此抛物线的解析式;
(2)若点![]() 是
是![]() 的中点,则求点
的中点,则求点![]() 的坐标;
的坐标;
(3)若以点![]() 为顶点的三角形与
为顶点的三角形与![]() 相似,请直接写出点
相似,请直接写出点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)P(
;(3)P(![]() ,
,![]() )或P(
)或P(![]() ,
,![]() )
)
【解析】
(1)把A点坐标和B点坐标代入![]() ,解方程组即可;
,解方程组即可;
(2)用m可表示出P、N的坐标,由题意可知有P为线段MN的中点,可得到关于m的方程,可求得m的值,即可求得点![]() 的坐标;
的坐标;
(3) 用m可表示出NP,PM,AM,分当∠BNP=90°时和当∠NBP=90°时两种情况讨论即可.
解: (1) 抛物线![]() 经过点
经过点![]()
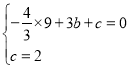 解得
解得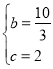
∴![]()
(2)由题意易得,直线![]() 的解析式为
的解析式为![]()
由![]() ,设
,设![]() ,
,![]()
则![]() ,
,![]()
点![]() 是
是![]() 的中点,即
的中点,即![]()
∴![]() ,解得
,解得![]() (舍)
(舍)
∴![]()
(3) ![]() .
.
由![]() ,设
,设![]() ,
,![]()
∴![]() ,
,![]() ,AM=3m,
,AM=3m,
∵△BPN和△APM相似,且∠BPN=∠APM,
∴∠BNP=∠AMP=90°或∠NBP=∠AMP=90°,
当∠BNP=90°时,则有BN⊥MN,
∴N点的纵坐标为2,
∴![]() =2,
=2,
解得m=0(舍去)或m=![]() ,
,
∴P(![]() ,
,![]() );
);
当∠NBP=90°时,过点N作NC⊥y轴于点C,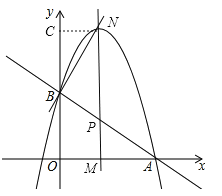
则∠NBC+∠BNC=90°,NC=m,BC=![]() 2=
2=![]() ,
,
∵∠NBP=90°,
∴∠NBC+∠ABO=90°,
∴∠ABO=∠BNC,
∴Rt△NCB∽Rt△BOA,
∴![]() ,
,
∴m2=![]() ,
,
解得m=0(舍去)或m=![]() ,
,
∴P(![]() ,
,![]() ),
),
综上可知,当以B,P,N为顶点的三角形与△APM相似时,点P的坐标为P(![]() ,
,![]() )或P(
)或P(![]() ,
,![]() ).
).


科目:初中数学 来源: 题型:
【题目】定义:在平面直角坐标系中,抛物线![]() (
(![]() )与直线
)与直线![]() 交于点
交于点![]() 、
、![]() (点
(点![]() 在点
在点![]() 右边),将抛物线
右边),将抛物线![]() 沿直线
沿直线![]() 翻折,翻折前后两抛物线的顶点分别为点
翻折,翻折前后两抛物线的顶点分别为点![]() 、
、![]() ,我们将两抛物线之间形成的封闭图形称为惊喜线,四边形
,我们将两抛物线之间形成的封闭图形称为惊喜线,四边形![]() 称为惊喜四边形,对角线
称为惊喜四边形,对角线![]() 与
与![]() 之比称为惊喜度(Degree of surprise),记作
之比称为惊喜度(Degree of surprise),记作![]() .
.
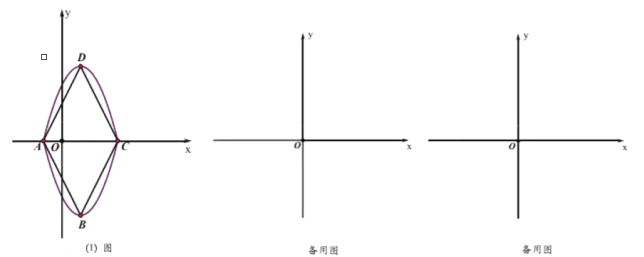
(1)如图(1)抛物线![]() 沿直线
沿直线![]() 翻折后得到惊喜线.则点
翻折后得到惊喜线.则点![]() 坐标 ,点
坐标 ,点![]() 坐标 ,惊喜四边形
坐标 ,惊喜四边形![]() 属于所学过的哪种特殊平行四边形? ,
属于所学过的哪种特殊平行四边形? ,![]() 为 .
为 .
(2)如果抛物线![]() (
(![]() )沿直线
)沿直线![]() 翻折后所得惊喜线的惊喜度为1,求
翻折后所得惊喜线的惊喜度为1,求![]() 的值.
的值.
(3)如果抛物线![]() 沿直线
沿直线![]() 翻折后所得的惊喜线在
翻折后所得的惊喜线在![]() 时,其最高点的纵坐标为16,求
时,其最高点的纵坐标为16,求![]() 的值并直接写出惊喜度
的值并直接写出惊喜度![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子中,装有除颜色外都完全相同的4个红球和若干个黄球.
![]() 如果从袋中任意摸出一个球是红球的概率为
如果从袋中任意摸出一个球是红球的概率为![]() ,那么袋中有黄球多少个?
,那么袋中有黄球多少个?
![]() 在
在![]() 的条件下如果从袋中摸出一个球记下颜色后放回,再摸出一个球,用列表或画树状图的方法求出两次摸出不同颜色球的概率.
的条件下如果从袋中摸出一个球记下颜色后放回,再摸出一个球,用列表或画树状图的方法求出两次摸出不同颜色球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=ax2+bx+c经过A(0,﹣4)和B(2,0)两点.
(1)求c的值及a,b满足的关系式;
(2)若抛物线在A和B两点间,从左到右上升,求a的取值范围;
(3)抛物线同时经过两个不同的点M(p,m),N(﹣2﹣p,n).
①若m=n,求a的值;
②若m=﹣2p﹣3,n=2p+1,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
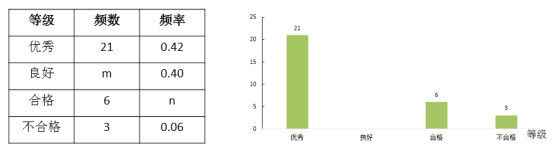
【题目】某学校开展了主题为“垃圾分类,绿色生活新时尚”的宣传活动,为了解学生对垃圾分类知识的掌握情况,该校环保社团成员在校园内随机抽取了部分学生进行问卷调查将他们的得分按优秀、良好、合格、不合格四个等级进行统计,并绘制了如下不完整的统计表和条形统计图.请根据图表信息,解答下列问题:
![]() 本次调查随机抽取了____ 名学生:表中
本次调查随机抽取了____ 名学生:表中![]() ;
;![]()
![]() 补全条形统计图:
补全条形统计图:
![]() 若全校有
若全校有![]() 名学生,请你估计该校掌握垃圾分类知识达到“优秀"和“良好”等级的学生共有多少人
名学生,请你估计该校掌握垃圾分类知识达到“优秀"和“良好”等级的学生共有多少人
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读以下材料,并按要求完成相应地任务:
莱昂哈德·欧拉(Leonhard Euler)是瑞士数学家,在数学上经常见到以他的名字命名的重要常数,公式和定理,下面是欧拉发现的一个定理:在△ABC中,R和r分别为外接圆和内切圆的半径,O和I分别为其外心和内心,则![]() .
.
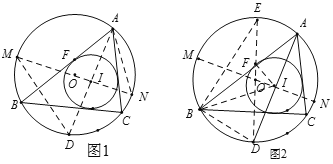
如图1,⊙O和⊙I分别是△ABC的外接圆和内切圆,⊙I与AB相切分于点F,设⊙O的半径为R,⊙I的半径为r,外心O(三角形三边垂直平分线的交点)与内心I(三角形三条角平分线的交点)之间的距离OI=d,则有d2=R2﹣2Rr.
下面是该定理的证明过程(部分):
延长AI交⊙O于点D,过点I作⊙O的直径MN,连接DM,AN.
∵∠D=∠N,∠DMI=∠NAI(同弧所对的圆周角相等),
∴△MDI∽△ANI,
∴![]() ,
,
∴![]() ①,
①,
如图2,在图1(隐去MD,AN)的基础上作⊙O的直径DE,连接BE,BD,BI,IF,
∵DE是⊙O的直径,∴∠DBE=90°,
∵⊙I与AB相切于点F,∴∠AFI=90°,
∴∠DBE=∠IFA,
∵∠BAD=∠E(同弧所对圆周角相等),
∴△AIF∽△EDB,
∴![]() ,∴
,∴![]() ②,
②,
任务:(1)观察发现:![]() ,
,![]() (用含R,d的代数式表示);
(用含R,d的代数式表示);
(2)请判断BD和ID的数量关系,并说明理由;
(3)请观察式子①和式子②,并利用任务(1),(2)的结论,按照上面的证明思路,完成该定理证明的剩余部分;
(4)应用:若△ABC的外接圆的半径为5cm,内切圆的半径为2cm,则△ABC的外心与内心之间的距离为 cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
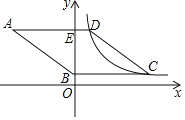
【题目】如图,菱形ABCD的边AD⊥y轴,垂足为点E,顶点A在第二象限,顶点B在y轴的正半轴上,反比例函数y=![]() (k≠0,x>0)的图象同时经过顶点C,D.若点C的横坐标为5,BE=3DE,则k的值为( )
(k≠0,x>0)的图象同时经过顶点C,D.若点C的横坐标为5,BE=3DE,则k的值为( )
A. ![]() B. 3 C.
B. 3 C. ![]() D. 5
D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的四枚邮票图片形状完全相同,分别是我国代科学家祖冲之、李时珍、张衡、僧一行.把四张图片混合在一起.

(1)若随机摸取一张图片,则摸到“祖冲之”图片的概率是__________;
(2)若随机摸取一张图片然后放回,再随机摸取一张图片,利用列表或树状图求两次至少有一次摸到“祖冲之”图片的概率;
(3)小东、小西、小南、小北四位同学依次摸取图片,若小东摸到“祖冲之”图片,则剩下三人中( )
A.小西摸到“李时珍”图片的概率大 B.小南摸到“李时珍”图片的概率大
C.小北摸到“李时珍”图片的概率大 D.三人摸到“李时珍”图片的概率一样大
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com