
【题目】某公园的门票价格如下表所示:
购票人数 | 1~50人 | 51~100人 | 100人以上 |
每人门票价 | 20元 | 17元 | 14元 |
某校初一(1)(2)两个班去游览公园,其中(1)班人数较少,不足50人,(2)班人数较多,超过50人,但是不超过100人.如果两个班都以班为单位分别购票,则一共应付1912元;如果两个班联合起来,作为个团体购票,则只需付1456元
(1)列方程或方程组求出两个班各有多少学生?
(2)若(1)班全员参加,(2)班有20人不参加此次活动,请你设计一种最省钱方式来帮他们买票,并说明理由.
(3)你认为是否存在这样的可能:51到100人之间买票的钱数与100人以上买票的钱数相等?如果有,是多少人与多少人买票钱数相等?(直接写结果)
【答案】(1)初一(1)班有48人,初一(2)班有56人;(2)两个班联合起来买101张门票最省钱;理由见解析;(3)84人和102人或98人和119人买票钱数相等.
【解析】
(1)由两班人数之和为整数可得出初一(1)(2)两个班的人数之和大于100,设初一(1)班有![]() 人,初一(2)班有y人,根据总价=单价×数量,即可得出二元一次方程组,解之即可;
人,初一(2)班有y人,根据总价=单价×数量,即可得出二元一次方程组,解之即可;
(2)求出参加活动的人数,利用总价=单价×数量,分别求出购买84张门票及101张门票所需钱数,比较后即可得出结论;
(3)设m人与n人买票钱数相等(51≤m≤100,n≥101),根据总价=单价×数量且总价相等,即可得出关于m,n的二元一次方程,结合m,n为正整数及其范围,即可求出m,n的值.
(1)如果初一(1)(2)两个班的人数之和不大于100,
则1456÷17=85(人)![]() (元),不符合题意,
(元),不符合题意,
∴初一(1)(2)两个班的人数之和大于100.
设初一(1)班有x人,初一(2)班有y人,
依题意,得: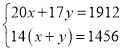 ,
,
解得:![]() ;
;
答:初一(1)班有48人,初一(2)班有56人;
(2)48+(56﹣20)=84(人).
两个班合起来买84张门票所需钱数为:84×17=1428(元),
两个班合起来买101张门票所需钱数为:101×14=1414(元),
∵1414<1428,
∴两个班合起来买101张门票最省钱;
(3)设m人与n人买票钱数相等(51≤m≤100,n≥101),
依题意,得:17m=14n,
∴m为14的整数倍,n为17的整数倍,
∴![]() 或
或![]() .
.
答:84人和102人或98人和119人买票钱数相等.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】用分式方程解决问题:元旦假期有两个小组去攀登- -座高h米的山,第二组的攀登速度是第- -组的a倍.
(1)若![]() ,两小组同时开始攀登,结果第二组比第一组早
,两小组同时开始攀登,结果第二组比第一组早![]() 到达顶峰.求两个小组的攀登速度.
到达顶峰.求两个小组的攀登速度.
(2)若第二组比第一组晚出发![]() ,结果两组同时到达顶峰,求第二组的攀登速度比第一组快多少? (用含
,结果两组同时到达顶峰,求第二组的攀登速度比第一组快多少? (用含![]() 的代数式表示)
的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
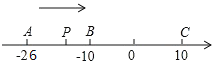
【题目】已知数轴上有A、B、C三点,分别表示有理数﹣26,﹣10,10,动点P从A出发,以每秒1个单位的速度向右移动,当P点运动到C点时运动停止,设点P移动时间为t秒。
(1)用含t的代数式表示P到点A和点C的距离:PA=_____,PC=_____.
(2)当点P运动到B点时,点Q从A出发,以每秒3个单位的速度向右运动,求t等于多少秒时P、Q两点相遇?t等于多少秒时P、Q两点相距4个单位长度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校组织团员举行申奥成功宣传活动,从学校骑车出发,先上坡到达A地后,宣传8分钟;然后下坡到B地宣传8分钟返回,行程情况如图.若返回时,上、下坡速度仍保持不变,在A地仍要宣传8分钟,那么他们从B地返回学校用的时间是( )

A. 45.2分钟 B. 48分钟 C. 46分钟 D. 33分钟
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC在平面直角坐标系中如图所示,
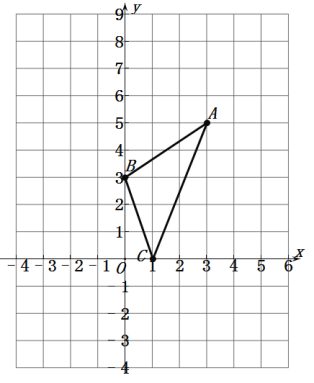
(1)S△ABC= .
(2)x轴上是否存在点P,使得S△BCP=2S△ABC,若不存在,说明理由;若存在,求出P点的坐标.
(3)请直接写出:以A、B、C为顶点的平行四边形的第四个顶点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数y =(2m+1) x+ m-3
(1) 若函数图象经过原点,求m的值.
(2) 若函数图象在y轴的交点的纵坐标为-2,求m的值.
(3)若函数的图象平行直线y=-3x–3,求m的值.
(4)若这个函数是一次函数,且y随着x的增大而减小,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
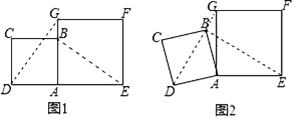
【题目】在数学兴趣小组活动中,小明进行数学探究活动.将边长为2的正方形ABCD与边长为3的正方形AEFG按图1位置放置,AD与AE在同一条直线上,AB与AG在同一条直线上.
(1)小明发现DG=BE且DG⊥BE,请你给出证明.
(2)如图2,小明将正方形ABCD绕点A逆时针旋转,当点B恰好落在线段DG上时,请你帮他求出此时△ADG的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,经过点A(6,0)的直线y=kx﹣3与直线y=﹣x交于点B,点P从点O出发以每秒1个单位长度的速度向点A匀速运动.
(1)求点B的坐标;
(2)当△OPB是直角三角形时,求点P运动的时间;
(3)当BP平分△OAB的面积时,直线BP与y轴交于点D,求线段BD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
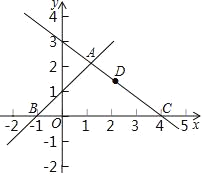
【题目】如图,在平面直角坐标系可中,直线y=x+1与y=﹣![]() x+3交于点A,分别交x轴于点B和点C,点D是直线AC上的一个动点.
x+3交于点A,分别交x轴于点B和点C,点D是直线AC上的一个动点.
(1)求点A,B,C的坐标;
(2)在直线AB上是否存在点E使得四边形EODA为平行四边形?存在的话直接写出![]() 的值,不存在请说明理由;
的值,不存在请说明理由;
(3)当△CBD为等腰三角形时直接写出D坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com