
【题目】已知,如图,矩形![]() 中,
中,![]() ,
,![]() ,菱形
,菱形![]() 的三个顶点
的三个顶点![]() ,
,![]() ,
,![]() 分别在矩形
分别在矩形![]() 的边
的边![]() ,
,![]() ,
,![]() 上,
上,![]() ,连接
,连接![]() .
.
(1)若![]() ,求证四边形
,求证四边形![]() 为正方形;
为正方形;
(2)若![]() ,求
,求![]() 的面积.
的面积.
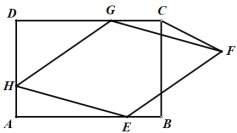
【答案】(1)见详解;(2)1
【解析】
(1)由于四边形ABCD为矩形,四边形HEFG为菱形,那么∠D=∠A=90°,HG=HE,而AH=DG=2,易证△AHE≌△DGH,从而有∠DHG=∠HEA,等量代换可得∠AHE+∠DHG=90°,易证四边形HEFG为正方形;
(2)过F作FM⊥DC,交DC延长线于M,连接GE,由于AB//CD,可得∠AEG=∠MGE,同理有∠HEG=∠FGE,利用等式性质有∠AEH=∠MGF,再结合∠A=∠M=90°,HE=FG,可证△AHE≌△MFG,从而有FM=HA=2,进而可求三角形面积.
解:(1)∵四边形ABCD为矩形,四边形HEFG为菱形,
∴∠D=∠A=90°,HG=HE,又AH=DG=2,
∴Rt△AHE≌Rt△DGH(HL),
∴∠DHG=∠HEA,
∵∠AHE+∠HEA=90°,
∴∠AHE+∠DHG=90°,
∴∠EHG=90°,
∴四边形HEFG为正方形;
(2)过F作FM⊥DC,交DC延长线于M,连接GE,
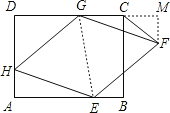
∵AB//CD,
∴∠AEG=∠MGE,
∵HE//GF,
∴∠HEG=∠FGE,
∴∠AEH=∠MGF,
在△AHE和△MFG中,∠A=∠M=90°,HE=FG,
∴△AHE≌△MFG,
∴FM=HA=2,即无论菱形EFGH如何变化,点F到直线CD的距离始终为定值2,
因此S△FCG=![]() ×FM×GC=
×FM×GC=![]() ×2×(76)=1.
×2×(76)=1.


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:初中数学 来源: 题型:
【题目】已知△ABC在平面直角坐标系中的位置如图所示:
(1)画出△ABC绕点A按逆时针方向旋转90°后的△A′B′C′;
(2)在(1)的条件下,求点C旋转到点C′所经过的路线长及线段AC旋转到新位置时所划过区域的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, AB与CD交于点O, OE⊥CD, OF⊥AB, ∠BOD=25°, 则∠AOE=______ , ∠DOF=______,∠AOC=______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的直径为10,在⊙O上位于直径AB的异侧有定点C和动点P,已知BC:CA=4:3,点P在半圆弧AB上运动(不与A、B两点重合),过点C作CP的垂线CD交PB的延长线于D点.
(1)求证:ACCD=PCBC;
(2)当点P运动到AB弧中点时,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“差之毫厘,失之千里”是一句描述开始时虽然相差很微小,结果会造成很大的误差或错误的成语.现实中就有这样的实例,如步枪在瞄准时的示意图如图,从眼睛到准星的距离OE为80cm,眼睛距离目标为200m,步枪上准星宽度AB为2mm,若射击时,由于抖动导致视线偏离了准星1mm,则目标偏离的距离为( )cm.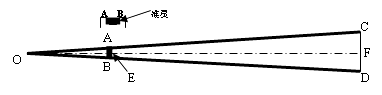
A.25
B.50
C.75
D.100
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点M是AB的中点,点P在MB上.分别以AP,PB为边,作正方形APCD和正方形PBEF,连结MD和ME.设AP=a,BP=b,且a+b=10,ab=20.则图中阴影部分的面积为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学初一年级有350名同学去春游,已知2辆A型车和1辆B型车可以载学生100人;1辆A型车和2辆B型车可以载学生110人.(1)A、B型车每辆可分别载学生多少人?(2)若租一辆A型车需要1000元,一辆B型车需1200元,请你设计租车方案,使得恰好运送完学生并且租车费用最少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市荸荠喜获丰收,某生产基地收获荸荠40吨.经市场调查,可采用批发、零售、加工销售三种销售方式,这三种销售方式每吨荸荠的利润如下表:
销售方式 批发 零售 加工销售
利润(百元/吨) 12 22 30
设按计划全部售出后的总利润为y百元,其中批发量为x吨,且加工销售量为15吨.
(1)求y与x之间的函数关系式;
(2)若零售量不超过批发量的4倍,求该生产基地按计划全部售完荸荠后获得的最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,抛物线y=ax2+bx+c的顶点为B(﹣1,3),与x轴的交点A在点(﹣3,0)和(﹣2,0)之间,以下结论: ①b2﹣4ac=0;②a+b+c>0;③2a﹣b=0;④c﹣a=3
其中正确的有( )
A.1
B.2
C.3
D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com