
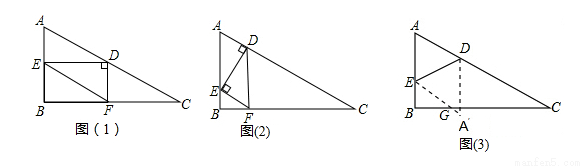
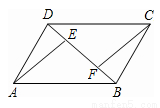
如图,已知在Rt△ABC中,∠ABC=90°,∠C=30°,AC=12cm,点E从点A出发沿AB以每秒1cm的速度向点B运动,同时点D从点C出发沿CA以每秒2cm的速度向点A运动,运动时间为t秒(0<t<6),过点D作DF⊥BC于点F.
(1)试用含t的式子表示AE、AD的长;
(2)如图①,在D、E运动的过程中,四边形AEFD是平行四边形,请说明理由;
(3)如图②,连接DE,当t为何值时,△DEF为直角三角形?
(4)如图③,将△ADE沿DE翻折得到△A′DE,试问当t为何值时,四边形AEA′D为菱形?

(1)AE=t,AD=12-2t;(2)理由见解析;(3)3或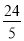 ;(4)4.
;(4)4.
【解析】
试题分析:(1)根据题意直接表示出来即可;
(2)由“在直角三角形中,30度角所对的直角边是斜边的一半”求得DF=t,又AE=t,则DF=AE;而由垂直得到AB∥DF,即“四边形AEFD的对边平行且相等”,由此得四边形AEFD是平行四边形.
(3)①显然∠DFE<90°;②当∠EDF=90°时,四边形EBFD为矩形,此时 AE=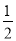 AD,根据题意,列出关于t的方程,通过解方程来求t的值;③当∠DEF=90°时,此时∠ADE=90°-∠A=30°,此时AD=
AD,根据题意,列出关于t的方程,通过解方程来求t的值;③当∠DEF=90°时,此时∠ADE=90°-∠A=30°,此时AD=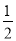 AE,根据题意,列出关于t的方程,通过解方程来求t的值.
AE,根据题意,列出关于t的方程,通过解方程来求t的值.
(4)如图③,若四边形AEA′D为菱形,则AE=AD,则t=12-2t,所以t=4.即当t=4时,四边形AEA′D为菱形.
(1)AE=t,AD=12-2t.
(2)∵DF⊥BC,∠C=30°,∴DF=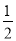 CD=
CD=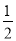 ×2t=t.
×2t=t.
∵AE=t,∴DF=AE.
∵∠ABC=90°,DF⊥BC,∴DF∥AE.
∴四边形AEFD是平行四边形.
(3)①显然∠DFE<90°.
②如图(1),当∠EDF=90°时,四边形EBFD为矩形,
此时 AE=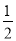 AD,∴t=
AD,∴t=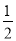 (12?2t).∴t=3.
(12?2t).∴t=3.
③如图(2),当∠DEF=90°时,此时∠ADE=90°,
∴∠AED=90°-∠A=30°.∴AD=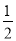 AE.∴12?2t=
AE.∴12?2t=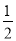 t.∴t=
t.∴t=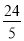 .
.
综上:当t=3秒或t=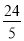 秒时,△DEF为直角三角形.
秒时,△DEF为直角三角形.
(4)如图(3),若四边形AEA′D为菱形,则AE=AD.
∴t=12-2t.∴t=4.
∴当t=4时,四边形AEA′D为菱形.
考点:1.双动点问题;2.矩形的性质;3.直角三角形的性质;4.菱形的性质;5.平行四边形的判定和性质;6.分类思想的应用.


 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:初中数学 来源:2015届黑龙江省八年级下学期期末考试数学试卷(解析版) 题型:选择题
如果一个直角三角形的两条边长分别是6和8,另一个与它相似的直角三角形边长分别是3和4及x,那么x的值( )
A.只有1个 B.可以有2个
C.有2个以上,但有限 D.有无数个
查看答案和解析>>
科目:初中数学 来源:2015届重庆市岩口复兴学校八年级下学期期中命题三数学试卷(解析版) 题型:选择题
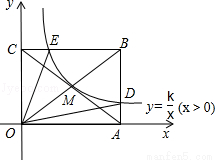
如图,反比例函数 (x>0)的图象经过矩形OABC对角线的交点M,分别于AB、BC交于点D、E,若四边形ODBE的面积为9,则k的值为( )
(x>0)的图象经过矩形OABC对角线的交点M,分别于AB、BC交于点D、E,若四边形ODBE的面积为9,则k的值为( )
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:初中数学 来源:2015届重庆市岩口复兴学校八年级下学期期中命题三数学试卷(解析版) 题型:选择题
若点P(2k-1,1-k)在第四象限,则k的取值范围为( )
A、k>1 B、k<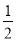 C、k>
C、k>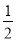 D、
D、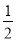 <k<1
<k<1
查看答案和解析>>
科目:初中数学 来源:2015届重庆市合川区第五学区八年级下学期半期考试数学试卷(解析版) 题型:解答题
如图所示,已知在平行四边形ABCD中,BE=DF.求证:∠DAE=∠BCF.
查看答案和解析>>
科目:初中数学 来源:2015届重庆市八年级下期期末考试数学试卷(解析版) 题型:解答题
某蔬菜店第一次用400元购进某种蔬菜,由于销售状况良好,该店又用700元第二次购进该品种蔬菜,所购数量是第一次购进数量的2倍,但进货价每千克少了0.5元.
(1)第一次所购该蔬菜的进货价是每千克多少元?
(2)蔬菜店在销售中,如果两次售价均相同,第一次购进的蔬菜有2% 的损耗,第二次购进的蔬菜有3% 的损耗,若该蔬菜店售完这些蔬菜获利不低于944元,则该蔬菜每千克售价至少为多少元?
查看答案和解析>>
科目:初中数学 来源:2015届辽宁省北票市八年级下学期期中考试数学试卷(解析版) 题型:选择题
利用因式分解简便计算57×99+44×99-99正确的是 ( )
A.99×(57+44)=99×101=9999
B.99×(57+44-1)=99×100=9900
C.99×(57+44+1)=99×102=100098
D.99×(57+44-99)=99 ×2=198
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com