
一次函数y=ax+b与二次函数y=ax2+bx+c在同一坐标系中的图象可能是( )
A.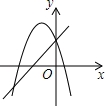 B.
B.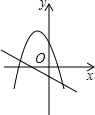 C.
C.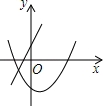 D.
D.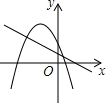
B【考点】二次函数的图象;一次函数的图象.
【分析】先由一次函数y=ax+b图象得到字母系数的正负,再与二次函数y=ax2+bx+c的图象相比较看是否一致.
【解答】解:A、由抛物线可知,a<0,x=﹣ <0,得b>0,由直线可知,a>0,b>0,故本选项
<0,得b>0,由直线可知,a>0,b>0,故本选项 错误;
错误;
B、由抛物线可知,a<0,x=﹣ <0,得b<0,由直线可知,a<0,b<0,故本选项正确;
<0,得b<0,由直线可知,a<0,b<0,故本选项正确;
C、由抛物线可知,a>0,x=﹣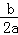 >0,得b<0,由直线可知,a>0,b>0,故本选项错误;
>0,得b<0,由直线可知,a>0,b>0,故本选项错误;
D、由抛物线可知,a<0,x=﹣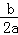 <0,得b<0,由直线可知,a>0,b>0,故本选项错误.
<0,得b<0,由直线可知,a>0,b>0,故本选项错误.
故选:B.
【点评】本题考查一次函数与二次函数的图象,掌握抛物线和直线的性质,用假设法来搞定这种数形结合题是一种很好的方法.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
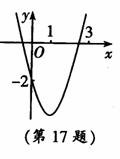
如图,已知抛物线y=x2+bx+c经过点(0,-2),请你确定
一个b的值,使该抛物线与x轴的一个交点在(1,0)和(3,0)之间.
你所确定的b的值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
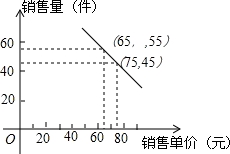
超市市场部整理出销售某品牌新款童装的销售量与销售单价的相关信息如下:
已知该童装的进价为每件60元,设销售单价为x元,销售单价不低于进价,且获利不得高于45%,设销售该款童装的利润为W元.
(1)求利润W与销售单价x之间的关系式,并求销售单价定为多少元时,商场可获得最大利润,最大利润是多少元?
(2)若超市销售该款童装获得的利润不低于500元,试确定销售单价x的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
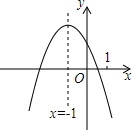
二次函数 y=ax2+bx+c(a≠0)的图象如图,给出下列四个结论:①4ac﹣b2<0;②4a+c<2b;③3b+2c<0;④abc>0,其中正确结论是__________.(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
某商品经过连续两次降价,销售单价由原来的125元降到80元.设平均每次降价的百分率为x,由题意列方程:( )
A.125(1﹣x)2=80 B.125(1﹣2x)=80 C.125(1﹣2x)2=80 D.80(1﹣x)2=125
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com