
【题目】如图:直线 a,b,c 表示三条相互交叉而建的公路,现在要建立一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有( )
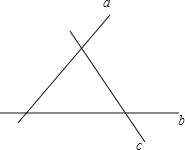
A. 1 个 B. 2 个 C. 3 个 D. 4 个
【答案】D
【解析】
本题要分类讨论的思想,从内角平分线和外角平分线两方面思考,首先由三角形内角平分线的交点到三角形三边的距离相等,可得三角形内角平分线的交点满足条件;再者利用角平分线的性质,可证得三角形两条外角平分线的交点到其三边的距离也相等,这样的点有3个,可得可供选择的地址有4个.
∵△ABC内角平分线的交点到三角形三边的距离相等,
∴△ABC内角平分线的交点满足条件;
如图:点P是△ABC两条外角平分线的交点,

过点P作PE⊥AB,PD⊥BC,PF⊥AC,
∴PE=PF,PF=PD,
∴PE=PF=PD,
∴点P到△ABC的三边的距离相等,
∴△ABC两条外角平分线的交点到其三边的距离也相等,满足这条件的点有3个;
综上,到三条公路的距离相等的点有4个,
∴可供选择的地址有4个.
故选:D.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】探究题:
(1)三条直线相交,最少有__________个交点,最多有__________个交点,分别画出图形,并数出图形中的对顶角和邻补角的对数;
(2)四条直线相交,最少有__________个交点,最多有__________个交点,分别画出图形,并数出图形中的对顶角和邻补角的对数;
(3)依次类推,n条直线相交,最少有__________个交点,最多有__________个交点,对顶角有__________对,邻补角有__________对.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按照如下步骤计算:6﹣2÷( ![]() +
+ ![]() ﹣
﹣ ![]() ﹣
﹣ ![]() ).
).
(1)计算:( ![]() +
+ ![]() ﹣
﹣ ![]() ﹣
﹣ ![]() )÷6﹣2;
)÷6﹣2;
(2)根据两个算式的关系,直接写出6﹣2÷( ![]() +
+ ![]() ﹣
﹣ ![]() ﹣
﹣ ![]() )的结果.
)的结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在三角板ABC中,∠ACB=90°,∠A=30°,AC=6,将三角板ABC绕点C逆时针旋转,当起始位置时的点B恰好落在边A1B1上时,A1B的长为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学开展“阳光体育一小时”活动,按学校实际情况,决定开设A:踢毽子;B:篮球;C:跳绳;D:乒乓球四种运动项目.为了解学生最喜欢哪一种运动项目,随机抽取了一部分学生进行调查,并将调查结果绘制成如下两个统计图.请结合图中的信息解答下列问题: 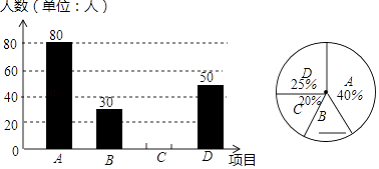
(1)本次共调查了名学生;
(2)在扇形统计图中,“B”所在扇形的圆心角是度;
(3)将条形统计图补充完整;
(4)若该中学有1200名学生,喜欢篮球运动的学生约有名.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线y=﹣x+3与x轴、y轴分别交于A,B两点,抛物线y=﹣x2+bx+c经过A,B两点,点P在线段OA上,从点A以1个单位/秒的速度匀速运动;同时,点Q在线段AB上,从点A出发,向点B以 ![]() 个单位/秒的速度匀速运动,连接PQ,设运动时间为t秒.
个单位/秒的速度匀速运动,连接PQ,设运动时间为t秒.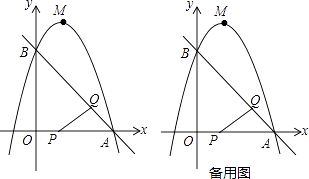
(1)求抛物线的解析式;
(2)当t为何值时,△APQ为直角三角形;
(3)过点P作PE∥y轴,交AB于点E,过点Q作QF∥y轴,交抛物线于点F,连接EF,当EF∥PQ时,求点F的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB,CD被直线EF所截,点G,H为它们的交点,∠AGE与它的同位角相等,HP平分∠GHD.∠AGH∶∠BGH=2∶7,试求∠CHG和∠PHD的度数.
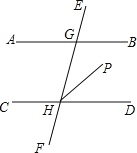
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列三行数,并完成后面的问题:
①-2,4,-8,16,……
②1,-2,4,-8,……
③0,-3,3,-9,……
(1)思考第①行数的规律,写出第![]() 个数字是________;
个数字是________;
(2)设第②行第![]() 个数为
个数为![]() 第③行第
第③行第![]() 个数为
个数为![]() 请直接写出
请直接写出![]() 与
与![]() 之间的关系;
之间的关系;
(3)设![]() 分别表示第①、②、③行数的第2019个数字,求
分别表示第①、②、③行数的第2019个数字,求![]() 的值。
的值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com