
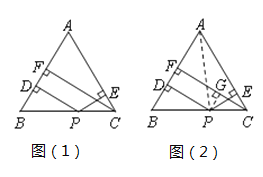
°Њћвƒњ°њ’≈јѕ ¶Єш∞ЃЇ√—Іѕ∞µƒµƒ–°ЊьЇЌ–°њ°ћб≥ц’в—щ“їЄцќ ћв£Ї»зЌЉ£®1£©£ђ‘Џ°чABC÷–£ђAB£љAC£ђµгPќ™±яBC…ѕµƒ»ќ“їµг£ђєэµгP„чPD°ЌAB£ђPE°ЌAC£ђіє„гЈ÷±рќ™D£ђE£ђєэµгC„чCF°ЌAB£ђіє„гќ™F£Ѓ«у÷§£ЇPD£ЂPE£љCF£Ѓ
–°Њьµƒ÷§√чЋЉ¬Ј «£Ї»зЌЉ£®2£©£ђЅђљ”AP£ђ”…°чABP”л°чACP√жїэ÷ЃЇЌµ»”Џ°чABCµƒ√жїэњ…“‘÷§µ√£ЇPD£ЂPE£љCF£Ѓ
јѕ ¶±н—пЅЋ–°Њь£ђ≤Ґ«“ЄжЋя–°ЊьЇЌ–°њ°£Ї‘Џ«уљв∆љ√жЉЄЇќќ ћвµƒ ±Їт£ђЄщЊЁ”–єЎЉЄЇќЅњ”л…жЉ∞µƒ”–єЎЌЉ–ќ√жїэ÷ЃЉдµƒƒЏ‘ЏЅ™ѕµ£ђ”√√жїэїт√жїэ÷ЃЉдµƒєЎѕµ±н Њ”–єЎѕяґќЉдµƒєЎѕµ£ђі”ґш∞—“™¬џ÷§µƒѕяґќ÷ЃЉдµƒєЎѕµ„™їѓќ™√жїэµƒєЎѕµ£ђ≤ҐЌ®єэЌЉ–ќ√жїэµƒµ»їэ±дїїґ‘Ћщ¬џќ ћвјіљш––«уљвµƒЈљЈ®£ђ’в÷÷ЈљЈ®≥∆ќ™°∞√жїэЈ®°±.
«лƒг є”√°∞√жїэЈ®°±љвЊцѕ¬Ѕ–ќ ћв£Ї
£®1£©Rt°чABCЅљћх÷±љ«±я≥§ќ™3ЇЌ4£ђ‘тЋьµƒƒЏ«–‘≤∞лЊґќ™ £ї
£®2£©»зЌЉ£®3£©£ђ°чABC÷–AB=15£ђBC=14£ђAC=13£ђAD «BC±я…ѕµƒЄя.«уAD≥§Љ∞°чABCµƒƒЏ«–‘≤µƒ∞лЊґ£ї
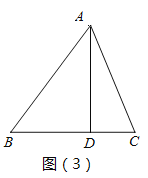
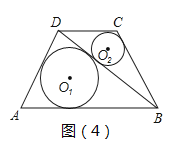
£®3£©»зЌЉ£®4£©£ђ‘ЏЋƒ±я–ќABCD÷–£ђ°—O1”л°—O2Ј÷±рќ™°чABD”л°чBCDµƒƒЏ«–‘≤£ђ°—O1”л°чABD«–µгЈ÷±рќ™E°ҐF°ҐG£ђ…иЋь√«µƒ∞лЊґЈ÷±рќ™r1ЇЌr2£ђ»ф°ѕADB=90°г£ђAE=8£ђBC+CD=20£ђS°чDBC=36£ђr2=2£ђ«уr1µƒ÷µ£Ѓ
°Њір∞Є°њ£®1£©1£ї£®2£©AD=12£ђƒЏ«–‘≤∞лЊґќ™4£ї£®3£©2.
°Њљвќц°њ
£®1£©”…єіє…ґ®јн«у≥ц![]() £ђ…и∞лЊґ «r£ђЄщЊЁ√жїэЈ®
£ђ…и∞лЊґ «r£ђЄщЊЁ√жїэЈ®
![]() £ђЈ÷±ріъ»лїѓЉтњ…µ√£ї
£ђЈ÷±ріъ»лїѓЉтњ…µ√£ї
£®2£©”…єіє…ґ®јнµ√![]() £ђіъ»л«у≥ц
£ђіъ»л«у≥ц![]() £ђ
£ђ
…и∞лЊґ «r £ђЄщЊЁ√жїэЈ®![]() £ђіъ»лїѓЉтњ…µ√£ї
£ђіъ»лїѓЉтњ…µ√£ї
£®3£©”…£®2£©њ…÷™£ђ…и∞лЊґ «r £ђЄщЊЁ√жїэЈ®њ…µ√ ![]() £ђ
£ђ
‘тјы”√“—÷™њ…“‘«у≥ц![]() £ђ°—O1 «°чABDµƒƒЏ«–‘≤£ђњ…÷™
£ђ°—O1 «°чABDµƒƒЏ«–‘≤£ђњ…÷™![]() £ђ
£ђ![]() £ђ
£ђ![]() £ђ…и
£ђ…и![]() £ђјы”√єіє…ґ®јнµ√
£ђјы”√єіє…ґ®јнµ√![]() £ђ‘тњ…µ√≥ц
£ђ‘тњ…µ√≥ц![]() £ђ
£ђ
![]() £ђіъ»л
£ђіъ»л![]() Љіњ…«у≥ц°£
Љіњ…«у≥ц°£
£®1£©
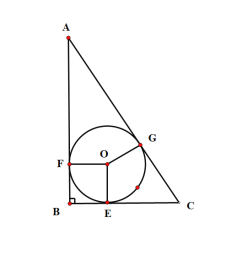
»зЌЉ Њ£ђRt°чABC÷–£ђAB=4£ђBC=3£ђ°—O «ƒЏ«–‘≤
°а![]()
…и°—Oµƒ∞лЊґ «r £ђ”…√жїэЈ®њ…µ√£Ї![]()
Љі£Ї![]()
°а![]()
°а![]()
°а![]()
£®2£©
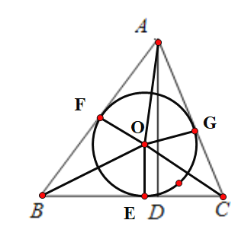
»зЌЉ Њ£ђ…и![]() £ђ‘т
£ђ‘т![]() £ђ≤Ґ«“AD «BC±я…ѕµƒЄя£ђ
£ђ≤Ґ«“AD «BC±я…ѕµƒЄя£ђ
°а”…єіє…ґ®јнµ√£Ї![]()
Љі£Ї![]() £ђ
£ђ
љв÷Ѓµ√£Ї![]()
°а![]() £ђ
£ђ![]() £ђ
£ђ![]()
°а…и°—Oµƒ∞лЊґ «r £ђ”…√жїэЈ®њ…µ√£Ї![]()
Љі£Ї![]()
°а![]()
љв÷Ѓµ√£Ї![]()
£®3£©
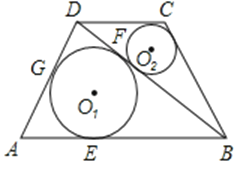
”…£®2£©њ…÷™£ђ…и∞лЊґ «r £ђЄщЊЁ√жїэЈ®њ…µ√£Ї![]()
Љі£Ї![]() £ђ
£ђ
“—÷™![]() £ђ
£ђ![]() £ђ
£ђ![]() £ђ
£ђ
°а![]() £ђЉі
£ђЉі![]() £ђ
£ђ
°я°—O1 «°чABDµƒƒЏ«–‘≤£ђ
°а![]() £ђ
£ђ![]() £ђ
£ђ![]() £ђ
£ђ
°а![]() £ђ
£ђ
°а…и![]() £ђ‘т
£ђ‘т![]() £ђ
£ђ![]() £ђ
£ђ![]() £ђ
£ђ
°я![]() £ђ
£ђ
°а![]() £ђЉі
£ђЉі![]() £ђ
£ђ
љвµ√![]() £ђ
£ђ
°а![]() £ђ
£ђ
![]()
°а


 »Ђƒ№ЅЈњЉЊнѕµЅ–ір∞Є
»Ђƒ№ЅЈњЉЊнѕµЅ–ір∞Є “їњќ“їЅЈњќ ±іп±кѕµЅ–ір∞Є
“їњќ“їЅЈњќ ±іп±кѕµЅ–ір∞Є
| ƒкЉґ | Єя÷–њќ≥ћ | ƒкЉґ | ≥х÷–њќ≥ћ |
| Єя“ї | Єя“ї√вЈ—њќ≥ћЌ∆Љц£° | ≥х“ї | ≥х“ї√вЈ—њќ≥ћЌ∆Љц£° |
| Єяґю | Єяґю√вЈ—њќ≥ћЌ∆Љц£° | ≥хґю | ≥хґю√вЈ—њќ≥ћЌ∆Љц£° |
| Єя»э | Єя»э√вЈ—њќ≥ћЌ∆Љц£° | ≥х»э | ≥х»э√вЈ—њќ≥ћЌ∆Љц£° |
њ∆ƒњ£Ї≥х÷– э—І јі‘і£Ї ћв–Ќ£Ї
°Њћвƒњ°њ£®12Ј÷£©»зЌЉ£ђЊЎ–ќABCD£ђAB£љ6cm£ђAD£љ2cm£ђµгP“‘2cm/sµƒЋўґ»і”ґ•µгA≥цЈҐ—Ў’џѕяA£≠B£≠CѕтµгC‘Ћґѓ£ђЌђ ±µгQ“‘lcm/sµƒЋўґ»і”ґ•µгC≥цЈҐѕтµгD‘Ћґѓ£ђµ±∆д÷–“їЄцґѓµгµљіпƒ©ґЋЌ£÷є‘Ћґѓ ±£ђЅн“їµг“≤Ќ£÷є‘Ћґѓ£Ѓ
 (1)ќ Ѕљґѓµг‘ЋґѓЉЄ√л£ђ єЋƒ±я–ќPBCQµƒ√жїэ «ЊЎ–ќABCD√жїэµƒ
(1)ќ Ѕљґѓµг‘ЋґѓЉЄ√л£ђ єЋƒ±я–ќPBCQµƒ√жїэ «ЊЎ–ќABCD√жїэµƒ![]() £ї
£ї
(2)ќ ЅљґѓµгЊ≠єэґа≥§ ±Љд єµ√µгP”лµгQ÷ЃЉдµƒЊајлќ™![]() £њ»фіж‘Џ£ђ
£њ»фіж‘Џ£ђ
«у≥ц‘ЋґѓЋщ–иµƒ ±Љд£ї»ф≤їіж‘Џ£ђ«лЋµ√чјн”…£Ѓ
≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£Ї≥х÷– э—І јі‘і£Ї ћв–Ќ£Ї
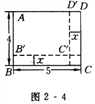
°Њћвƒњ°њ»зЌЉ2 - 4Ћщ Њ£ђ≥§Јљ–ќABCDµƒ≥§ќ™5 cm£ђњнќ™4 cm£ђ»зєыљЂЋьµƒ≥§ЇЌњнґЉЉх»•x(cm)£ђƒ«√іЋь £ѕ¬µƒ–°≥§Јљ–ќAB°дC°дD°дµƒ√жїэќ™y(cm2)£Ѓ
(1)–і≥цy”лxµƒЇѓ эєЎѕµ љ£ї
(2)…ѕ цЇѓ э « ≤√іЇѓ э?
(3)„‘±дЅњxµƒ»°÷µЈґќІ « ≤√і?
≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£Ї≥х÷– э—І јі‘і£Ї ћв–Ќ£Ї
°Њћвƒњ°њЋƒ±я–ќABCD÷–£ђAB=BC£ђ°ѕB=°ѕC=90°г£ђP «BC±я…ѕ“їµг£ђAP°ЌPD£ђE «AB±я…ѕ“їµг£ђ°ѕBPE=°ѕBAP£Ѓ
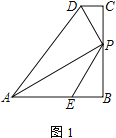
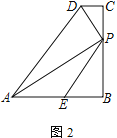
£®1£© »зЌЉ1£ђ»фAE=PE£ђ÷±љ”–і≥ц![]() =______£ї
=______£ї
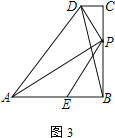
£®2£© »зЌЉ2£ђ«у÷§£ЇAP=PD£ЂPE£ї
£®3£© »зЌЉ3£ђµ±AE=BP ±£ђЅђBD£ђ‘т![]() =______£ђ≤ҐЋµ√чјн”…£Ѓ
=______£ђ≤ҐЋµ√чјн”…£Ѓ
≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£Ї≥х÷– э—І јі‘і£Ї ћв–Ќ£Ї
°Њћвƒњ°њ“—÷™єЎ”Џxµƒ“ї‘™ґюіќЈљ≥ћ(a£Ђc)x2£Ђ2bx£Ђ(a£≠c)£љ0£ђ∆д÷–a£ђb£ђcЈ÷±рќ™°чABC»э±яµƒ≥§£Ѓ
(1)»зєыx£љ£≠1 «Јљ≥ћµƒЄщ£ђ ‘≈–ґѕ°чABCµƒ–ќ„і£ђ≤ҐЋµ√чјн”…£ї
(2)»зєыЈљ≥ћ”–ЅљЄцѕаµ»µƒ µ эЄщ£ђ ‘≈–ґѕ°чABCµƒ–ќ„і£ђ≤ҐЋµ√чјн”…£Ѓ
≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£Ї≥х÷– э—І јі‘і£Ї ћв–Ќ£Ї
°Њћвƒњ°њ»ф≈„ќпѕяy=x2+bx(b>2)…ѕіж‘ЏєЎ”Џ÷±ѕяy=x≥…÷бґ‘≥∆µƒЅљЄцµг£ђ‘тbµƒ»°÷µЈґќІ «______.
≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£Ї≥х÷– э—І јі‘і£Ї ћв–Ќ£Ї
°Њћвƒњ°њ“—÷™£Ї»зЌЉ£ђЊЎ–ќABCDµƒґ‘љ«ѕяACµƒіє÷±∆љЈ÷ѕяEF”лAD°ҐAC°ҐBCЈ÷±рљї”ЏµгE°ҐO°ҐF£Ѓ
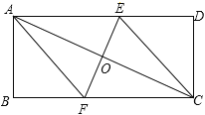
£®1£©«у÷§£ЇЋƒ±я–ќAFCE «Ѕв–ќ£ї
£®2£©»фAB=5£ђBC=12£ђEF=6£ђ«уЅв–ќAFCEµƒ√жїэ£Ѓ
≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£Ї≥х÷– э—І јі‘і£Ї ћв–Ќ£Ї
°Њћвƒњ°њ»зЌЉ£ђ≈„ќпѕяy=©Бx2+bx+c£®a°ў0£©”лx÷бљї”ЏµгA£®©Б1£ђ0£©ЇЌB£®3£ђ0£©£ђ”лy÷бљї”ЏµгC£ђµгDµƒЇб„ш±кќ™m£®0£Љm£Љ3£©£ђЅђљбDC≤Ґ—”≥§÷ЅE£ђ єµ√CE=CD£ђЅђљбBE£ђBC£Ѓ
£®1£©«у≈„ќпѕяµƒљвќц љ£ї
£®2£©”√Їђmµƒіъ э љ±н ЊµгEµƒ„ш±к£ђ≤Ґ«у≥цµгE„Ё„ш±кµƒЈґќІ£ї
£®3£©«у°чBCEµƒ√жїэ„оіу÷µ£Ѓ

≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£Ї≥х÷– э—І јі‘і£Ї ћв–Ќ£Ї
°Њћвƒњ°њµгP «’эЈљ–ќABCD±яAB…ѕ“їµг£®≤ї”лA£ђB÷ЎЇѕ£©£ђЅђљ”PD≤ҐљЂѕяґќPD»∆µгPЋ≥ ±’л–э„™90°г£ђµ√µљѕяґќPE£ђЅђљ”BE£ђ‘т°ѕCBEµ»”Џ £Ѓ
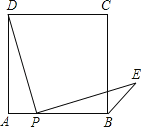
≤йњіір∞ЄЇЌљвќц>>
єъЉ —І–£”≈—° - ЅЈѕ∞≤бЅ–±н - ‘ћвЅ–±н
Їю±± °ї•Ѕ™Ќшќ•Ј®ЇЌ≤їЅЉ–≈ѕҐЊў±®∆љћ® | Ќш…ѕ”–Ї¶–≈ѕҐЊў±®„®«ш | µз–≈’©∆≠Њў±®„®«ш | …жјъ Ј–йќё÷ч“е”–Ї¶–≈ѕҐЊў±®„®«ш | …ж∆у«÷»®Њў±®„®«ш
ќ•Ј®ЇЌ≤їЅЉ–≈ѕҐЊў±®µзї∞£Ї027-86699610 Њў±®” ѕд£Ї58377363@163.com