
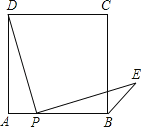
【题目】点P是正方形ABCD边AB上一点(不与A,B重合),连接PD并将线段PD绕点P顺时针旋转90°,得到线段PE,连接BE,则∠CBE等于 .
【答案】45°
【解析】
试题在AD上取一点F,使DF=BP,连接PF,由正方形的性质就可以得出△DFP≌△PBE,就可以得出∠DFP=∠PBE,根据AP=AF就可以得出∠DFP的值,就可以求出∠CBE的值.
解:在AD上取一点F,使DF=BP,连接PF,
∵四边形ABCD是正方形,
∴AD=AB,∠A=∠ABC=90°.
∴AD﹣DF=AB﹣BP,∠ADP+∠APD=90°,
∴AF=AP.
∴∠AFP=∠APF=45°,
∴∠DFP=135°.
∵∠DPE=90°
∴∠APD+∠BPE=90°.
∴∠ADP=∠BPE.
在△DFP和△PBE中,
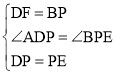 ,
,
∴△DFP≌△PBE(SAS),
∴∠DFP=∠PBE,
∴∠PBE=135°,
∴∠EBC=135°﹣90°=45°.
故答案为:45°.


科目:初中数学 来源: 题型:
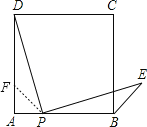
【题目】张老师给爱好学习的的小军和小俊提出这样一个问题:如图(1),在△ABC中,AB=AC,点P为边BC上的任一点,过点P作PD⊥AB,PE⊥AC,垂足分别为D,E,过点C作CF⊥AB,垂足为F.求证:PD+PE=CF.
小军的证明思路是:如图(2),连接AP,由△ABP与△ACP面积之和等于△ABC的面积可以证得:PD+PE=CF.
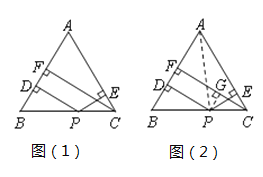
老师表扬了小军,并且告诉小军和小俊:在求解平面几何问题的时候,根据有关几何量与涉及的有关图形面积之间的内在联系,用面积或面积之间的关系表示有关线段间的关系,从而把要论证的线段之间的关系转化为面积的关系,并通过图形面积的等积变换对所论问题来进行求解的方法,这种方法称为“面积法”.
请你使用“面积法”解决下列问题:
(1)Rt△ABC两条直角边长为3和4,则它的内切圆半径为 ;
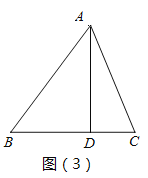
(2)如图(3),△ABC中AB=15,BC=14,AC=13,AD是BC边上的高.求AD长及△ABC的内切圆的半径;
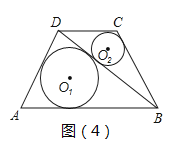
(3)如图(4),在四边形ABCD中,⊙O1与⊙O2分别为△ABD与△BCD的内切圆,⊙O1与△ABD切点分别为E、F、G,设它们的半径分别为r1和r2,若∠ADB=90°,AE=8,BC+CD=20,S△DBC=36,r2=2,求r1的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
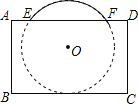
【题目】把球放在长方体纸盒内,球的一部分露出盒外,其主视图如图.⊙O与矩形ABCD的边BC,AD分别相切和相交(E,F是交点),已知EF=CD=8,则⊙O的半径为
查看答案和解析>>
科目:初中数学 来源: 题型:
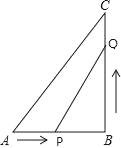
【题目】已知:如图所示.在△ABC中,∠B=90°,AB=5cm,BC=7cm.点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动,当其中一点达到终点后,另外一点也随之停止运动.
(1)如果P,Q分别从A,B同时出发,那么几秒后,△PBQ的面积等于4cm2?
(2)如果P,Q分别从A,B同时出发,那么几秒后,PQ的长度等于5cm?
(3)在(1)中,△PQB的面积能否等于7cm2?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情境:如图1,在正方形ABCD中,E为边BC上一点(不与点B、C重合),垂直于AE的一条直线MN分别交AB、AE、CD于点M、P、N.判断线段DN、MB、EC之间的数量关系,并说明理由.
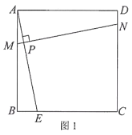
问题探究:在“问题情境”的基础上,
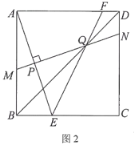
(1)如图2,若垂足P恰好为AE的中点,连接BD,交MN于点Q,连接EQ,并延长交边AD于点F.求∠AEF的度数;
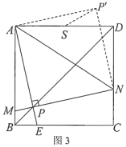
(2)如图3,当垂足P在正方形ABCD的对角线BD上时,连接AN,将△APN沿着AN翻折,点P落在点P'处.若正方形ABCD的边长为4 ,AD的中点为S,求P'S的最小值.
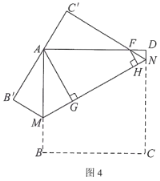
问题拓展:如图4,在边长为4的正方形ABCD中,点M、N分别为边AB、CD上的点,将正方形ABCD沿着MN翻折,使得BC的对应边B'C'恰好经过点A,C'N交AD于点F.分别过点A、F作AG⊥MN,FH⊥MN,垂足分别为G、H.若AG=![]() ,请直接写出FH的长.
,请直接写出FH的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列图形都是由同样大小的菱形按照一定规律组成的,请根据排列规律完成下列问题:
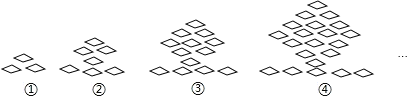
(1)填写下表:
图形序号 | 菱形个数 |
| 3 |
| 7 |
| ______ |
| ______ |
|
|
(2)根据表中规律猜想,图n中菱形的个数![]() 用含n的式子表示,不用说理
用含n的式子表示,不用说理![]() ;
;
(3)是否存在一个图形恰好由91个菱形组成?若存在,求出图形的序号;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
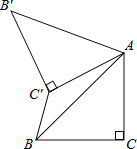
【题目】如图,已知△ABC中,∠C=90°,AC=BC=2![]() ,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,连接C′B,则C′B的长为_____.
,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,连接C′B,则C′B的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,平行四边形ACDE的一边在直径AB上,点E在⊙O上.

(1)如图1,当点D在⊙O上时,请你仅用无刻度的直尺在AB上取点P,使DP⊥AB于P;
(2)如图2,当点D在⊙O内时,请你仅用无刻度的直尺在AB上取点Q,使EQ⊥AB于Q.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com