
【题目】如图,点A(1,2)在反比例函数![]() 上,B为反比例函数图象上一点,不与A重合,当以OB为直径的圆经过A点,点B的坐标为___________.
上,B为反比例函数图象上一点,不与A重合,当以OB为直径的圆经过A点,点B的坐标为___________.
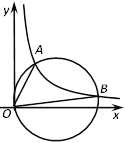
【答案】(4,0.5)
【解析】
将点A(1,2)代入![]() ,求得反比例函数解析式为
,求得反比例函数解析式为![]() ,设点B
,设点B![]() ,连接AB,过点A作x轴的平行线,交y轴于点C,过点B作y轴的平行线,交直线AC于点D,则∠OCA=∠D=90°,根据OB为圆的直径,∠OAB=90°,容易得到△AOC∽△BAD,所以有
,连接AB,过点A作x轴的平行线,交y轴于点C,过点B作y轴的平行线,交直线AC于点D,则∠OCA=∠D=90°,根据OB为圆的直径,∠OAB=90°,容易得到△AOC∽△BAD,所以有![]() ,即:
,即: 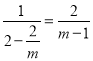 ,化简求值即可.
,化简求值即可.
解:将点A(1,2)代入![]() ,得:
,得:![]() ,
,
则反比例函数解析式为![]() ,
,
设点B![]()
如图,连接AB,过点A作x轴的平行线,交y轴于点C,过点B作y轴的平行线,交直线AC于点D,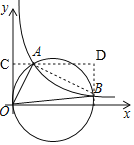
则∠OCA=∠D=90°,
∴∠AOC+∠OAC=90°,
∵OB为圆的直径,
∴∠OAB=90°,
∴∠OAC+∠BAD=90°,
∴∠AOC=∠BAD,
则△AOC∽△BAD,
∴![]() ,即:
,即: 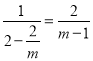 ,
,
解得:m=1(舍)或m=4,
则点B点坐标为:(4,0.5).


 提分百分百检测卷系列答案
提分百分百检测卷系列答案科目:初中数学 来源: 题型:
【题目】用适当的方法解下列方程:
(1)(x-1)2﹣9=0;
(2)3(x+5)=(x+5)2;
(3)x2+6x-55=0;
(4)2x(x+3)-1=0.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将平行四边形ABCD的边DC延长到点E,使CE=DC,连接AE,交BC于点F.
(1)求证:AC=BE;
(2)若∠AFC=2∠D,连接AC,BE.求证:四边形ABEC是矩形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果店销售一种水果的成本价是![]() 元/千克.在销售过程中发现,当这种水果的价格定在
元/千克.在销售过程中发现,当这种水果的价格定在![]() 元/千克时,每天可以卖出
元/千克时,每天可以卖出![]() 千克.在此基础上,这种水果的单价每提高
千克.在此基础上,这种水果的单价每提高![]() 元/千克,该水果店每天就会少卖出
元/千克,该水果店每天就会少卖出![]() 千克.
千克.
![]() 若该水果店每天销售这种水果所获得的利润是
若该水果店每天销售这种水果所获得的利润是![]() 元,则单价应定为多少?
元,则单价应定为多少?
![]() 在利润不变的情况下,为了让利于顾客,单价应定为多少?
在利润不变的情况下,为了让利于顾客,单价应定为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
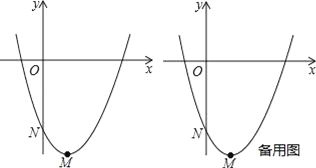
【题目】已知抛物线l:y=ax2+bx+c(a,b,c均不为0)的顶点为M,与y轴的交点为N,我们称以N为顶点,对称轴是y轴且过点M的抛物线为抛物线l的衍生抛物线,直线MN为抛物线l的衍生直线.
(1)如图,抛物线y=x2﹣2x﹣3的衍生抛物线的解析式是 ,衍生直线的解析式是 ;
(2)若一条抛物线的衍生抛物线和衍生直线分别是y=﹣2x2+1和y=﹣2x+1,求这条抛物线的解析式;
(3)如图,设(1)中的抛物线y=x2﹣2x﹣3的顶点为M,与y轴交点为N,将它的衍生直线MN先绕点N旋转到与x轴平行,再沿y轴向上平移1个单位得直线n,P是直线n上的动点,是否存在点P,使△POM为直角三角形?若存在,求出所有点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=﹣x2+2x+3的顶点为D,它与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C.
(1)求顶点D的坐标;
(2)求直线BC的解析式;
(3)求△BCD的面积;
(4)当点P在直线BC上方的抛物线上运动时,△PBC的面积是否存在最大值?若存在,请求出这个最大值,并且写出此时点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
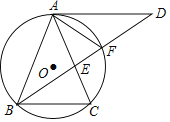
【题目】如图,△ABC内接于⊙O,AB=AC,∠BAC=36°,过点A作AD∥BC,与∠ABC的平分线交于点D,BD与AC交于点E,与⊙O交于点F.
(1)求∠DAF的度数;
(2)求证:AE2=EFED;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com