
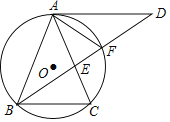
【题目】如图,△ABC内接于⊙O,AB=AC,∠BAC=36°,过点A作AD∥BC,与∠ABC的平分线交于点D,BD与AC交于点E,与⊙O交于点F.
(1)求∠DAF的度数;
(2)求证:AE2=EFED;
【答案】(1)36°;(2)证明见解析
【解析】
(1)求出∠ABC、∠ABD、∠CBD的度数,求出∠D度数,根据三角形内角和定理求出∠BAF和∠BAD度数,即可求出答案;
(2)求出△AEF∽△DEA,根据相似三角形的性质得出即可.
(1)∵AD∥BC,
∴∠D=∠CBD,
∵AB=AC,∠BAC=36°,
∴∠ABC=∠ACB=![]() ×(180°﹣∠BAC)=72°,
×(180°﹣∠BAC)=72°,
∴∠AFB=∠ACB=72°,
∵BD平分∠ABC,
∴∠ABD=∠CBD=![]() ∠ABC=
∠ABC=![]() ×72°=36°,
×72°=36°,
∴∠D=∠CBD=36°,
∴∠BAD=180°﹣∠D﹣∠ABD=180°﹣36°﹣36°=108°,
∠BAF=180°﹣∠ABF﹣∠AFB=180°﹣36°﹣72°=72°,
∴∠DAF=∠DAB﹣∠FAB=108°﹣72°=36°;
(2)∵∠CBD=36°,∠FAC=∠CBD,
∴∠FAC=36°=∠D,
∵∠AED=∠AEF,
∴△AEF∽△DEA,
∴![]() ,
,
∴AE2=EF×ED.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:
【题目】如图是一副眼镜镜片下半部分轮廓对应的两条抛物线关于y轴对称.AB∥x轴,AB=4cm,最低点C在x轴上,高CH=1cm,BD=2cm.则右轮廓线DFE所在抛物线的函数解析式为__________________________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,平行四边形ACDE的一边在直径AB上,点E在⊙O上.

(1)如图1,当点D在⊙O上时,请你仅用无刻度的直尺在AB上取点P,使DP⊥AB于P;
(2)如图2,当点D在⊙O内时,请你仅用无刻度的直尺在AB上取点Q,使EQ⊥AB于Q.
查看答案和解析>>
科目:初中数学 来源: 题型:
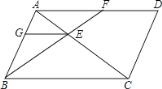
【题目】如图,平行四边形ABCD中,过点B的直线与对角线AC、边AD分别交于点E和F.过点E作EG∥BC,交AB于G,则图中相似三角形有( )
A. 7对 B. 6对 C. 5对 D. 4对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售一种商品,成本每千克40元,规定每千克售价不低于成本,且不高于80元,经市场调查,每天的销售量y(千克)与每千克售价x(元)满足一次函数关系,部分数据如下表:

(1)求y与x之间的函数表达式;
(2)设商品每天的总利润为W(元),求W与x之间的函数表达式(利润=收入-成本);
(3)试说明(2)中总利润W随售价x的变化而变化的情况,并指出售价为多少元时获得最大利润,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是边长为4的正三角形,以AB边作正方形ABDE,点P和点Q分别是线段AC和线段BC上的中点,连接AQ和BP相交于点M,则点M到DE的距离是_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com