
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+c的图象与x轴交于A(4,0),B两点,与y轴交于点C(0,2),对称轴x=1,与x轴交于点H.
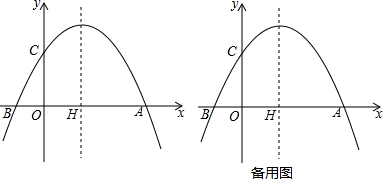
(1)求抛物线的函数表达式;
(2)直线y=kx+1(k≠0)与y轴交于点E,与抛物线交于点 P,Q(点P在y轴左侧,点Q在y轴右侧),连接CP,CQ,若△CPQ的面积为![]() ,求点P,Q的坐标;
,求点P,Q的坐标;
(3)在(2)的条件下,连接AC交PQ于G,在对称轴上是否存在一点K,连接GK,将线段GK绕点G顺时针旋转90°,使点K恰好落在抛物线上,若存在,请直接写出点K的坐标;若不存在,请说明理由.
【答案】(1)y=![]() ;(2)点P、Q的坐标分别为:(
;(2)点P、Q的坐标分别为:(![]() ,
,![]() )、(
)、(![]() ,﹣
,﹣![]() );(3)存在,点K(1,
);(3)存在,点K(1,![]() ).
).
【解析】
(1)根据对称轴x=1,求出点B的坐标,再将点B代入抛物线表达式中求出a的值,即可求抛物线的函数表达式;
(2)设直线PQ交y轴于点E(0,1),点P、Q横坐标分别为m,n,联立抛物线与直线PQ的表达式可得方程,求解方程即可得出点P,Q的坐标;
(3)设点K(1,m),联立PQ和AC的表达式,即可求出G点的坐标,过点G作x轴的平行线交函数对称轴于点M,交过点R与y轴的平行线于点N,通过△KMG≌△GNR可得R(m﹣1,![]() ),将R点代入抛物线解析式即可求出m的值,求得K的坐标.
),将R点代入抛物线解析式即可求出m的值,求得K的坐标.
(1)对称轴x=1,则点B(﹣2,0),
则抛物线的表达式为:y=a(x+2)(x﹣4)=a(x2﹣2x﹣8),
即﹣8a=2,
解得:a=![]() ,
,
故抛物线的表达式为:y=![]() ;
;
(2)设直线PQ交y轴于点E(0,1),点P、Q横坐标分别为m,n,

△CPQ的面积=![]() ×CE×(n﹣m)=
×CE×(n﹣m)=![]() ,即n﹣m=2
,即n﹣m=2![]() ,
,
联立抛物线与直线PQ的表达式并整理得:![]() …①,
…①,
m+n=2﹣4k,mn=﹣4,
n﹣m=2![]() =
=![]() =
=![]() ,
,
解得:k=0(舍去)或1;
将k=1代入①式并解得:x=![]() ,
,
故点P、Q的坐标分别为:(![]() ,
,![]() )、(
)、(![]() ,﹣
,﹣![]() )
)
(3)设点K(1,m),
联立PQ和AC的表达式并解得:x=![]() ,故点G(
,故点G(![]() ,
,![]() )
)
过点G作x轴的平行线交函数对称轴于点M,交过点R与y轴的平行线于点N,
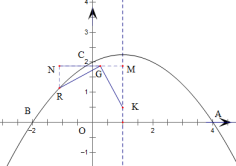
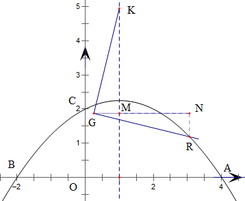
则△KMG≌△GNR(AAS),
GM=1-![]() =
=![]() =NR,MK=
=NR,MK=![]() ,
,
故点R的纵坐标为:![]() ,则点R(m﹣1,
,则点R(m﹣1,![]() )
)
将该坐标代入抛物线表达式解得:x=![]() ,
,
故m=![]() ,
,
故点K(1,![]() ).
).


科目:初中数学 来源: 题型:
【题目】在⊙O中,AB为直径,C为⊙O上一点.

(1)如图1,过点C作⊙O的切线,与AB延长线相交于点P,若∠CAB=27°,求∠P的度数;
(2)如图2,D为弧AB上一点,OD⊥AC,垂足为E,连接DC并延长,与AB的延长线交于点P,若∠CAB=10°,求∠P的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,甲、乙两人分别从![]() 两地出发,相向而行,已知甲先出发4分钟后,乙才出发,他们两人在
两地出发,相向而行,已知甲先出发4分钟后,乙才出发,他们两人在![]() 之间的
之间的![]() 地相遇,相遇后,甲立即返回
地相遇,相遇后,甲立即返回![]() 地,乙继续向
地,乙继续向![]() 地前行.甲到达
地前行.甲到达![]() 地时停止行走,乙到达
地时停止行走,乙到达![]() 地是也停止行走,在整个行走过程中,甲、乙两人均保持各自的速度匀速行走,甲、乙两人相距的路程
地是也停止行走,在整个行走过程中,甲、乙两人均保持各自的速度匀速行走,甲、乙两人相距的路程![]() (米)与甲出发的时间
(米)与甲出发的时间![]() (分钟)之间的关系如图所示,则下列结论错误的是( )
(分钟)之间的关系如图所示,则下列结论错误的是( )
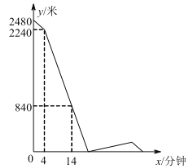
A.![]() 两地相距2480米B.甲的速度是60米/分钟,乙的速度是80米/分钟
两地相距2480米B.甲的速度是60米/分钟,乙的速度是80米/分钟
C.乙出发17分钟后,两人在![]() 地相遇D.乙到达
地相遇D.乙到达![]() 地时,甲与
地时,甲与![]() 地相距的路程是300米.
地相距的路程是300米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表给出了代数式﹣x2+bx+c与x的一些对应值:
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | … |
﹣x2+bx+c | … | 5 | n | c | 2 | ﹣3 | ﹣10 | … |
(1)根据表格中的数据,确定b,c,n的值;
(2)设y=﹣x2+bx+c,直接写出0≤x≤2时y的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,点E是BC边上一动点(不与点C重合)对角线AC与BD相交于点O,连接AE,交BD于点G.
(1)根据给出的△AEC,作出它的外接圆⊙F,并标出圆心F(不写作法和证明,保留作图痕迹);
(2)在(1)的条件下,连接EF.①求证:∠AEF=∠DBC;
②记t=GF2+AGGE,当AB=6,BD=6![]() 时,求t的取值范围.
时,求t的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=mx+4的图象与x轴相交于点A,与反比例函数y=![]() (x>0)的图象相交于点B(1,6).
(x>0)的图象相交于点B(1,6).
(1)求一次函数和反比例函数的解析式;
(2)设点P是x轴上一点,若S△APB=18,直接写出点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
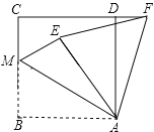
【题目】如图,在正方形ABCD中,AB=4,M是BC中点,连接AM,将△ABM沿AM折叠得到△AEM,将△ABM绕点A顺时针旋转90°得到△ADF,连接EF,则EF的长为( )
A.2![]() B.
B.![]() C.4D.2
C.4D.2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
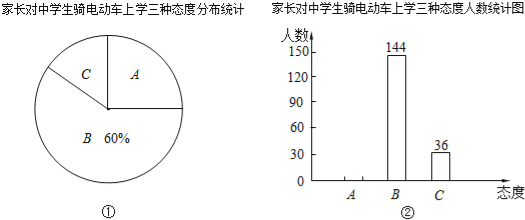
【题目】中学生骑电动车上学的现象越来越受到社会的关注.某市记者随机调查了一些家长对这种现象的态度(A:无所谓;B:反对;C:赞成),并将调査结果绘制成图①和图②的统计图(不完整).请根据图中提供的信息,解答下列问题:
(1)在图①中,C部分所占扇形的圆心角度数为 °;选择图①进行统计的优点是 ;
(2)将图②补充完整;
(3)根据抽样调查结果,请你估计该市50000名中学生家长中有多少名家长持赞成态度?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com