
【题目】如图,在菱形ABCD中,点E是BC边上一动点(不与点C重合)对角线AC与BD相交于点O,连接AE,交BD于点G.
(1)根据给出的△AEC,作出它的外接圆⊙F,并标出圆心F(不写作法和证明,保留作图痕迹);
(2)在(1)的条件下,连接EF.①求证:∠AEF=∠DBC;
②记t=GF2+AGGE,当AB=6,BD=6![]() 时,求t的取值范围.
时,求t的取值范围.

【答案】(1)见解析(2)①证明见解析②9≤t≤12
【解析】
(1)作EC的垂直平分线,其与BD的交点即为外心F;
(2)连接AF,EF,利用菱形的性质及外心的定义可证明∠DBC=90°﹣∠ACB及∠AEF=90°﹣∠ACB,可推出结论;
(3)先证△ABG∽△FEG,再证△EFB∽△GFE,由相似三角形的性质可推出t=GF2+AGGE=GF2+GFBG=GF(GF+BG)=GFBF=EF2,在菱形ABCD中,AC⊥BD,EF=AF≥AO,∴EF2≥AO2=32=9,当点F与点O重合时,AF最大,求出此时t的最大值为12,即可写出t的取值范围.
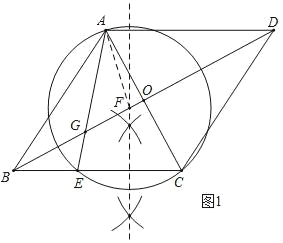
解:(1)如图1,⊙F为所求作的圆;
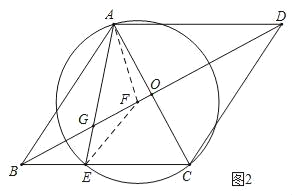
(2)①证明:
如图2,连接AF,EF,
∵四边形ABCD为菱形,
∴AC⊥BD,
∴∠DBC=90°﹣∠ACB,
∵FA=FE,
∴∠AEF=∠FAE,
∴∠AEF=![]() (180°﹣∠AFE)=90°﹣
(180°﹣∠AFE)=90°﹣![]() ∠AFE,
∠AFE,
又∠ACB=![]() ∠AFE,
∠AFE,
∴∠AEF=90°﹣∠ACB,
又∵∠DBC=90°﹣∠ACB,
∴∠AEF=∠DBC;
②解:∵四边形ABCD为菱形,
∴∠ABD=∠CBD,AO=CO,BO=DO=![]() BD=
BD=![]() ×
×![]() ,
,
在Rt△ABO中,AO=![]() ,
,
又∵∠AGB=∠FGE,∠ABG=∠FEG,
∴△ABG∽△FEG,
![]() ,
,
∴AGGE=GFBG,
∵∠GEF=∠FBE,∠GFE=∠EFB,
∴△EFB∽△GFE,
∴![]() ,
,
∴GFBF=EF2,
∴t=GF2+AGGE=GF2+GFBG=GF(GF+BG)=GFBF=EF2,
在菱形ABCD中,AC⊥BD,EF=AF≥AO,
∴EF2≥AO2=32=9,
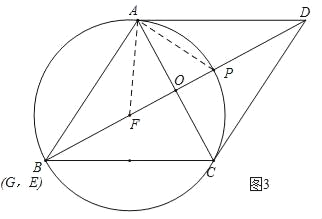
如图3,当点F与点O重合时,AF最大,
由题意可知:AF=BF,设AF=x,则OF=3![]() ﹣x,
﹣x,
∵AO2+OF2=AF2,
∴32+(3![]() ﹣x)2=x2,
﹣x)2=x2,
解得,x=2![]() ,
,
∴当x=2![]() 时,t的最大值为12,
时,t的最大值为12,
∴9≤t≤12.


科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E为 BC上的点,F为 CD边上的点,且AE=AF,AB=4,设EC=x,△AEF 的面积为y,则y与x之间的函数关系式是____.

查看答案和解析>>
科目:初中数学 来源: 题型:
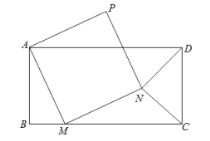
【题目】如图,已知矩形![]() ,点
,点![]() 为线段
为线段![]() 上一动点,沿线段
上一动点,沿线段![]() 由
由![]() 向
向![]() 运动,连接
运动,连接![]() ,以
,以![]() 为边向右侧作正方形
为边向右侧作正方形![]() ,连接
,连接![]() ,设
,设![]() 的路程即
的路程即![]() 的长为
的长为![]() ,
,![]() 间的距离为
间的距离为![]() ,
,![]() 间的距离为
间的距离为![]() .
.
数学兴趣小组的小刚根据学习函数的经验,分别对函数![]() 随自变量
随自变量![]() 的变化而变化的规律进行探究,过程如下:
的变化而变化的规律进行探究,过程如下:
(1)根据下表中自变量![]() 的取值进行去电,画图,测量,分别得到几组对应值,请将表格补充完成.
的取值进行去电,画图,测量,分别得到几组对应值,请将表格补充完成.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 3 | 2.22 |
| 3 | 4.11 | 5.39 | 6.72 |
| 4.24 | 2.81 | 1.39 | 0 |
| 2.84 | 4.26 |
其中,![]() ,
,![]() ;
;
(2)在同一平面黄子佼坐标系中,描点![]() ,并画出
,并画出![]() 的函数图像;
的函数图像;
(3)当![]() 为等腰三角形时,
为等腰三角形时,![]() 的长度约为 .
的长度约为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角梯形ABCD中,∠B=90°,AD∥BC,且AD=4cm,AB=6cm,DC=10cm.若动点P从A点出发,以每秒4cm的速度沿线段AD、DC向C点运动;动点Q从C点出发以每秒5cm的速度沿CB向B点运动,当Q点到达B点时,动点P、Q同时停止运动.设点P、Q同时出发,并运动了t秒.
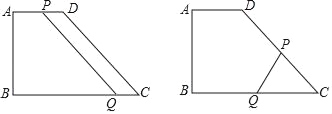
(1)当t为多少秒时,四边形PQCD是平行四边形?请说明理由;
(2)当t为多少秒时,AQ=DC?请说明理由;
(3)当t为多少秒时,PQ⊥DC?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+c的图象与x轴交于A(4,0),B两点,与y轴交于点C(0,2),对称轴x=1,与x轴交于点H.
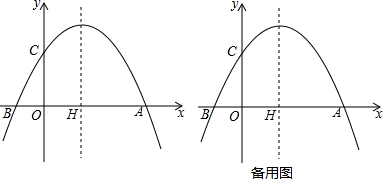
(1)求抛物线的函数表达式;
(2)直线y=kx+1(k≠0)与y轴交于点E,与抛物线交于点 P,Q(点P在y轴左侧,点Q在y轴右侧),连接CP,CQ,若△CPQ的面积为![]() ,求点P,Q的坐标;
,求点P,Q的坐标;
(3)在(2)的条件下,连接AC交PQ于G,在对称轴上是否存在一点K,连接GK,将线段GK绕点G顺时针旋转90°,使点K恰好落在抛物线上,若存在,请直接写出点K的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,当α=0°时,正方形ABCD与正方形AEFG互相重合,现将正方形AEFG绕点A逆时针旋转,当α=_____时(0°<α<360°),正方形AEFG的顶点F会落在正方形ABCD的两对角线AC或BD所在直线上.
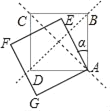
查看答案和解析>>
科目:初中数学 来源: 题型:
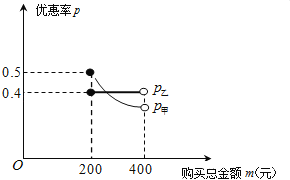
【题目】元旦期间,甲、乙两家商场都进行了促销活动,如何才能更好地衡量钏销对消费者受益程度的大小呢?某数学小组通过合作探究发现用优惠率p=![]() (其中k代表优惠金额,m代表顾客购买商品的总金额)可以很好地进行衡量,优惠率p越大,消费者受益程度越大;反之就越小.经统计,若顾客在甲、乙两家商场购买商品的总金额都为m(200≤m<400)元时,优惠率分别为P甲=
(其中k代表优惠金额,m代表顾客购买商品的总金额)可以很好地进行衡量,优惠率p越大,消费者受益程度越大;反之就越小.经统计,若顾客在甲、乙两家商场购买商品的总金额都为m(200≤m<400)元时,优惠率分别为P甲=![]() 与P乙=
与P乙=![]() ,它们与m的关系图象如图所示,其中p甲与m成反比例函数关系,p乙保持定值.
,它们与m的关系图象如图所示,其中p甲与m成反比例函数关系,p乙保持定值.
(1)求出k甲的值,并用含m的代数式表示k乙.
(2)当购买总金额m(元)在200≤m<400的条件下时,指出甲、乙两家商场正在采取的促销方案分别是什么.
(3)品牌、质量、规格等都相同的基本种商品,在甲、乙两家商场的标价都是m(200≤m<400)元,你认为选择哪家商场购买该商品花钱少些?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班到毕业时共结余班费1800元,班委会决定拿出一部分钱为老师购买纪念品,其余用于毕业晚会上给全班50位同学每人购买一件文化衫或者一本留言册作为纪念,了解到每件文化衫比每本留言册多8元,用200元恰好能购买4件文化衫和2本留言册.
(1)求买一件文化衫、一本留言册各需多少元?
(2)如果用于给老师买纪念品的钱数不少于120元,则这50件纪念品(每人一件文化衫或一本留言册)中最多能买多少件文化衫?
查看答案和解析>>
科目:初中数学 来源: 题型:
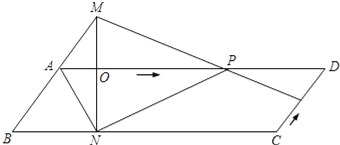
【题目】已知:如图,ABCD中,AD=3cm,CD=1cm,∠B=45°,点P从点A出发,沿AD方向匀速运动,速度为3cm/s;点Q从点C出发,沿CD方向匀速运动,速度为1cm/s,连接并延长QP交BA的延长线于点M,过M作MN⊥BC,垂足是N,设运动时间为t(s)(0<t<1).
(1)当t为何值时,四边形AQDM是平行四边形?
(2)证明:在P、Q运动的过程中,总有CQ=AM;
(3)是否存在某一时刻t,使四边形ANPM的面积是平行四边形ABCD的面积的一半?若存在,求出相应的t值;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com