
【题目】(猜想) 如图1,已知△ABC是等腰直角三角形,∠BAC=90°,点D是BC的中点.作正方形DEFG,使点A,C分别在DG和DE上,连接AE,BG.试猜想线段BG和AE的数量关系是 ;
(探究) 如图2,正方形DEFG绕点D逆时针旋转α(0°<α<360°).试判断你猜想的结论是否仍然成立,请利用图2证明你的结论;
(应用) 在图2中,BC=DE=4.当AE取最大值时,AF的值为多少?

【答案】【猜想】 BG=AE;【探究】成立,证明详见解析;【应用】 2![]() .
.
【解析】
【猜想】
:由等腰直角三角形的性质及正方形的性质就可以得出△ADE≌△BDG就可以得出结论;
【探究】如图2,连接AD,由等腰直角三角形的性质及正方形的性质就可以得出△ADE≌△BDG就可以得出结论;
【应用】可知BG=AE,当BG取得最大值时,AE取得最大值,由勾股定理就可以得出结论.
解:【猜想】 如图1,
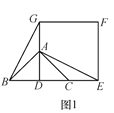
∵△ABC是等腰直角三角形,∠BAC=90°,点D是BC的中点,
∴AD⊥BC,BD=CD=AD,
∴∠ADB=∠ADC=90°.
∵四边形DEFG是正方形,
∴DE=DG.
在△BDG和△ADE中,
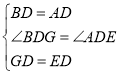 ,
,
∴△ADE≌△BDG(SAS),
∴BG=AE.
故答案为:BG=AE;
【探究】
成立,BG=AE.理由如下:
如图2,连接AD.
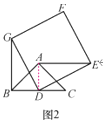
∵在Rt△BAC中,D为斜边BC的中点,
∴AD=BD,AD⊥BC.
∴∠ADG+∠GDB=90°.
∵四边形EFGD为正方形,
∴DE=DG,且∠GDE=90°.
∴∠ADG+∠ADE=90°.
∴∠BDG=∠ADE.
在△BDG和△ADE中,
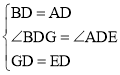
∴△BDG≌△ADE(SAS).
∴BG=AE.
【应用】
∵BG=AE,
∴当BG取得最大值时,AE取得最大值.
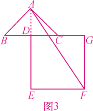
如图3,当旋转角为270°时,BG=AE.
∵BC=DE=4,
∴BG=2+4=6.
∴AE=6.
在Rt△AEF中,由勾股定理,得
AF=![]() =
=![]() =2
=2![]() .
.


科目:初中数学 来源: 题型:
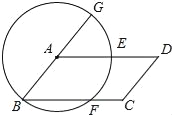
【题目】如图所示,以□ABCD的顶点A为圆心,AB为半径作圆,分别交AD,BC于点E,F,延长BA交⊙A于G.
(1)求证:弧GE=弧EF;
(2)若弧BF的度数为70°,求∠C的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
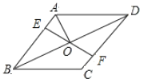
【题目】如图,在菱形ABCD中,点E,F分别在AB,CD上,且![]() ,连接EF交BD于点O连接AO.若
,连接EF交BD于点O连接AO.若![]() ,,则
,,则![]() 的度数为( )
的度数为( )
A.50°B.55°C.65°D.75°
查看答案和解析>>
科目:初中数学 来源: 题型:
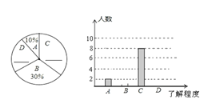
【题目】2018年5月31日是第31个“世界无烟日”,校学生会书记小明同学就“戒烟方式”的了解程度对本校九年级学生进行了一次随机问卷调查,下图是他采集数据后绘制的两幅不完整的统计图(A:了解较多,B:不了解,C:了解一点,D:非常了解).请你根据图中提供的信息解答以下问题:
(1)在扇形统计图中的横线上填写缺失的数据,并把条形统计图补充完整.
(2)2018年该初中九年级共有学生400人,按此调查,可以估计2018年该初中九年级学生中对戒烟方式“了解较多”以上的学生约有多少人?
(3)在问卷调查中,选择“A”的是1名男生,1名女生,选择“D”的有2名女生.校学生会要从选择“A、D”的问卷中,分别抽一名学生参加活动,请你用列表法或树状图求出恰好是一名男生一名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解下列方程:
(1)(y+2)2-(3y-1)2=0;
(2)5(x-3)2=x2-9;
(3)t2-![]() t+
t+![]() =0.
=0.
(4)2x2+7x+3=0(配方法).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水产养殖户进行小龙虾养殖. 已知每千克小龙虾养殖成本为6元,在整个销售旺季的80天里,日销售量![]() 与时间第
与时间第![]() 天之间的函数关系式为
天之间的函数关系式为![]() (
(![]() ,
,![]() 为整数),销售单价
为整数),销售单价![]() (元/
(元/![]() )与时间第
)与时间第![]() 天之间满足一次函数关系如下表:
天之间满足一次函数关系如下表:
时间第 | 1 | 2 | 3 | … | 80 |
销售单价 | 49. 5 | 49 | 48. 5 | … | 10 |
(1)写出销售单价![]() (元/
(元/![]() )与时间第
)与时间第![]() 天之间的函数关系式;
天之间的函数关系式;
(2)在整个销售旺季的80天里,哪一天的日销售利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A在线段BD上,在BD的同侧作等腰Rt△ABC和等腰Rt△ADE,其中∠ABC=∠AED=90°,CD与BE、AE分别交于点P、M.对于下列结论:①△CAM∽△DEM;②CD=2BE;③MPMD=MAME;④2CB2=CPCM.其中正确的是( )

A. ①②B. ①②③C. ①②③④D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某大学生创业团队有研发、管理和操作三个小组,各组的日工资和人数如下表所示.现从管理组分别抽调1人到研发组和操作组,调整后与调整前相比,下列说法中不正确的是( )
操作组 | 管理组 | 研发组 | |
日工资(元/人) | 260 | 280 | 300 |
人数(人) | 4 | 4 | 4 |
A.团队平均日工资不变B.团队日工资的方差不变
C.团队日工资的中位数不变D.团队日工资的极差不变
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=-x2+2x+m+1交x轴于点A(a,0)和B(b,0),交y轴于点C,抛物线的顶点为D,下列四个判断:①当x>0时,y>0;②若a=-1,则b=3;③抛物线上有两点P(x1,y1)和Q(x2,y2),若x1<1<x2,且x1+x2>2,则y1>y2;④点C关于抛物线对称轴的对称点为E,点G、F分别在x轴和y轴上,当m=2时,四边形EDGF周长的最小值为![]() ,其中,判断正确的序号是( )
,其中,判断正确的序号是( )

A.①②B.②③C.①③D.②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com