
【题目】解不等式组![]() .
.
(1)直接写出不等式组的解集 ,并求出它的整数解;
(2)有四张不透明的卡分别写上上面的整数解,随机抽出一张并放回再抽出一张,求出两次整数的和,请用列表或画树形图,求出两次的和为﹣1的概率.
【答案】(1)﹣3<x≤1,整数解为:﹣2,﹣1,0,1;(2)两次的和为﹣1的概率为![]() .
.
【解析】
(1)先求得不等式组中每一个不等式的解集,然后取其交集;根据不等式组的解集来求该不等式的整数集;
(2)根据题意先画出树状图得出所有等情况数和两次的和为﹣1的情况,然后根据概率公式即可得出答案.
(1)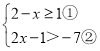 ,不等式①的解集为:x≤1;
,不等式①的解集为:x≤1;
不等式②的解集为:x>﹣3.
则原不等式的解集为:﹣3<x≤1,故该不等式的整数解为:﹣2,﹣1,0,1.
故答案为:﹣3<x≤1,整数解为:﹣2,﹣1,0,1;
(2)根据题意画树状图如下:

共有16种等可能的结果数,其中两次的和为﹣1的有4种结果,∴两次的和为﹣1的概率为![]() .
.


科目:初中数学 来源: 题型:
【题目】在国家政策的宏观调控下,某市的商品房成交均价由今年3月份的14 000元/m2下降到5月份的12 600元/m2.
(1)问4,5两月平均每月降价的百分率约是多少?(参考数据:![]() ≈0.95)
≈0.95)
(2)如果房价继续跌落,按此降价的百分率,你预测到7月份该市的商品房成交均价是否会跌跛10 000元/m2?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某建筑物,从10m高的窗口A,用水管向外喷水,喷出的水呈抛物线状(抛物线所在的平面与墙面垂直),如图所示,如果抛物线的最高点M离墙1m,离地面![]() m,则水流落地点B离墙的距离OB是( )
m,则水流落地点B离墙的距离OB是( )
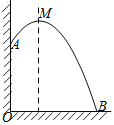
A.2mB.3mC.4mD.5m
查看答案和解析>>
科目:初中数学 来源: 题型:
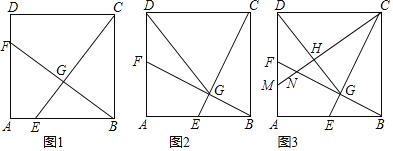
【题目】如图1,在正方形![]() 中,点
中,点![]() 是
是![]() 边上的一个动点(点
边上的一个动点(点![]() 与点
与点![]() 不重合),连接
不重合),连接![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .
.
(1)求证:![]() ;
;
(2)如图2,当点![]() 运动到
运动到![]() 中点时,连接
中点时,连接![]() ,求证:
,求证:![]() ;
;
(3)如图3,在(2)的条件下,过点![]() 作
作![]() 于点
于点![]() ,分别交
,分别交![]() 于点
于点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
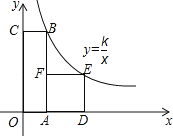
【题目】如图,四边形OABC是矩形,ADEF是正方形,点A、D在x轴的正半轴上,点C在y轴的正半轴上,点F在AB上,点B,E在反比例函数y=![]() 的图象上,OA=1,OC=6,试求出正方形ADEF的边长.
的图象上,OA=1,OC=6,试求出正方形ADEF的边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线C1:y=(x+![]() )2,平移抛物线y=﹣x2,使其顶点D在抛物线C1位于y轴右侧的图象上,得到抛物线C2,抛物线C2交x轴于A、B两点(点A在点B的左侧),交y轴于点C,设点D的横坐标为a.
)2,平移抛物线y=﹣x2,使其顶点D在抛物线C1位于y轴右侧的图象上,得到抛物线C2,抛物线C2交x轴于A、B两点(点A在点B的左侧),交y轴于点C,设点D的横坐标为a.

(1)当OC=2时,求抛物线C2的解析式;
(2)在抛物线的C2的对称轴上是否存在一点P,使得AP+CP的长最短?若存在,求出点P的坐标(用含a的代数式表示);若不存在,请说明理由;
(3)在(2)的条件下,连接OP,若OP⊥BC,求此时a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如果一元二次方程![]() 满足
满足![]() ,那么我们称这个方程为“凤凰”方程.已知
,那么我们称这个方程为“凤凰”方程.已知![]() 是“凤凰”方程,且有两个相等的实数根,则下列结论正确的是 ( )
是“凤凰”方程,且有两个相等的实数根,则下列结论正确的是 ( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知菱形ABCD的边长为2![]() ,点A在x轴负半轴上,点B在坐标原点。点D的坐标为(
,点A在x轴负半轴上,点B在坐标原点。点D的坐标为(![]() ,3),抛物线y=ax2+b(a≠0)经过AB、CD两边的中点.
,3),抛物线y=ax2+b(a≠0)经过AB、CD两边的中点.
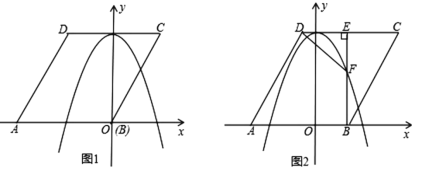
(1)求这条抛物线的函数解析式;
(2)将菱形ABCD以每秒1个单位长度的速度沿x轴正方向匀速平移(如图2),过点B作BE⊥CD于点E,交抛物线于点F,连接DF.设菱形ABCD平移的时间为t秒(0<t<3)
①是否存在这样的t,使DF=![]() FB?若存在,求出t的值;若不存在,请说明理由;
FB?若存在,求出t的值;若不存在,请说明理由;
②连接FC,以点F为旋转中心,将△FEC按顺时针方向旋转180°,得△FE′C′,当△FE′C′落在x轴与抛物线在x轴上方的部分围成的图形中(包括边界)时,求t的取值范围.(直接写出答案即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
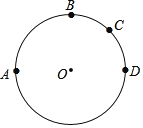
【题目】如图所示A、B、C、D四点在⊙O上的位置,其中![]() =180°,且
=180°,且![]() =
=![]() ,
,![]() =
=![]() .若阿超在
.若阿超在![]() 上取一点P,在
上取一点P,在![]() 上取一点Q,使得∠APQ=130°,则下列叙述何者正确( )
上取一点Q,使得∠APQ=130°,则下列叙述何者正确( )
A. Q点在![]() 上,且
上,且![]() >
>![]() B. Q点在
B. Q点在![]() 上,且
上,且![]() <
<![]()
C. Q点在![]() 上,且
上,且![]() >
>![]() D. Q点在
D. Q点在![]() 上,且
上,且![]() <
<![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com