Question

9．如图1，O为直线AB上一点，过点O作射线OC，∠AOC=30°，将一直角三角板（∠M=30°）的直角顶点放在点O处，一边ON在射线OA上，另一边OM与OC都在直线AB的上方．
（1）将图1中的三角板绕点O以每秒3°的速度沿顺时针方向旋转一周．如图2，经过t秒后，OM恰好平分∠BOC．①求t的值；②此时ON是否平分∠AOC？请说明理由；
（2）在（1）问的基础上，若三角板在转动的同时，射线OC也绕O点以每秒6°的速度沿顺时针方向旋转一周，如图3，那么经过多长时间OC平分∠MON？请说明理由；
（3）在（2）问的基础上，经过多长时间OC平分∠MOB？请画图并说明理由．

Answer 1

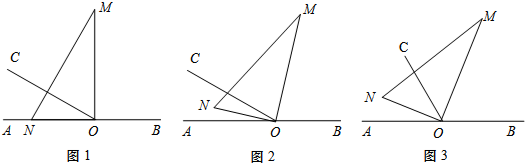
分析 （1）根据图形和题意得出∠AON+∠BOM=90°，∠CON+∠COM=90°，再根据∠AON=∠CON，即可得出OM平分∠BOC；
（2）根据图形和题意得出∠AON+∠BOM=90°，∠CON=∠COM=45°，再根据转动速度从而得出答案；
（3）分别根据转动速度关系和OC平分∠MOB画图即可．

解答 解：（1）①∵∠AON+∠BOM=90°，∠COM=∠MOB，
∵∠AOC=30°，
∴∠BOC=2∠COM=150°，
∴∠COM=75°，
∴∠CON=15°，
∴∠AON=∠AOC-∠CON=30°-15°=15°，
解得：t=15°÷3°=5秒；
②是，理由如下：
∵∠CON=15°，∠AON=15°，
∴ON平分∠AOC；
（2）5秒时OC平分∠MON，理由如下：
∵∠AON+∠BOM=90°，∠CON=∠COM，
∵∠MON=90°，
∴∠CON=∠COM=45°，
∵三角板绕点O以每秒3°的速度，射线OC也绕O点以每秒6°的速度旋转，
设∠AON为3t，∠AOC为30°+6t，
∵∠AOC-∠AON=45°，
可得：6t-3t=15°，
解得：t=5秒；
（3）OC平分∠MOB
∵∠AON+∠BOM=90°，∠BOC=∠COM，
∵三角板绕点O以每秒3°的速度，射线OC也绕O点以每秒6°的速度旋转，
设∠AON为3t，∠AOC为30°+6t，
∴∠COM为$\frac{1}{2}$（90°-3t），
∵∠BOM+∠AON=90°，
可得：180°-（30°+6t）=$\frac{1}{2}$（90°-3t），
解得：t=$\frac{70}{3}$秒；
如图：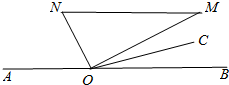

点评 此题考查了角的计算，关键是应该认真审题并仔细观察图形，找到各个量之间的关系求出角的度数是解题的关键．