
【题目】如图,在![]() 中,AB为
中,AB为![]() 的直径,C为
的直径,C为![]() 上一点,P是
上一点,P是![]() 的中点,过点P作AC的垂线,交AC的延长线于点D.
的中点,过点P作AC的垂线,交AC的延长线于点D.

(1)求证:DP是![]() 的切线;
的切线;
(2)若AC=5,![]() ,求AP的长.
,求AP的长.
【答案】(1)见解析;(2)AP=![]() .
.
【解析】
(1)根据题意连接OP,直接利用切线的定理进行分析证明即可;
(2)根据题意连接BC,交于OP于点G,利用三角函数和勾股定理以及矩形的性质进行综合分析计算即可.
解:(1)证明:连接OP;
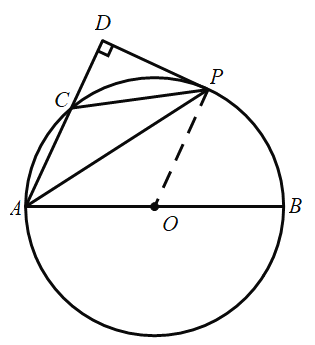
∵OP=OA;
∴∠1=∠2;
又∵P为![]() D的中点;
D的中点;
∴![]()
∴∠1=∠3;
∴∠3=∠2;
∴OP∥DA;
∵∠D=90°;
∴∠OPD=90°;
又∵OP为O半径;
∴DP为O的切线;
(2)连接BC,交于OP于点G;
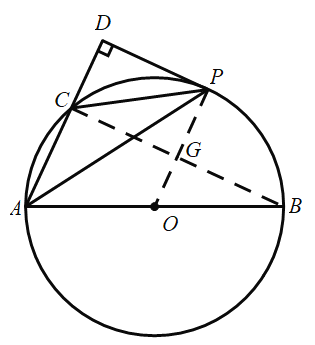
∵AB是圆O的直径;
∴∠ACB为直角;
∵![]()
∴sin∠ABC=![]()
AC=5,则AB=13,半径为![]()
由勾股定理的BC=![]() ,那么CG=6
,那么CG=6
又∵四边形DCGP为矩形;
∴GP=DC=6.5-2.5=4
∴AD=5+4=9;
在Rt△ADP中,AP=![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,扇形AOB,且OB=4,∠AOB=90°,C为弧AB上任意一点,过C点作CD⊥OB于点D,设△ODC的内心为E,连接OE、CE,当点C从点B运动到点A时,内心E所经过的路径长为 ________.
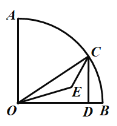
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在半径为6的⊙O中,正六边形ABCDEF与正方形AGDH都内接于⊙O,则图中阴影部分的面积为( )
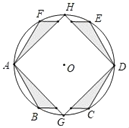
A. 27﹣9![]() B. 18
B. 18![]() C. 54﹣18
C. 54﹣18![]() D. 54
D. 54
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,以![]() 的边
的边![]() 为直径作
为直径作![]() ,点
,点![]() 在
在![]() 上,
上,![]() 是
是![]() 的弦,
的弦,![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() .
.
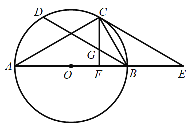
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)求证:![]() ;
;
(3)若![]() ,CG=4,求
,CG=4,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形![]() 中,已知
中,已知![]() ,
,![]() ,点
,点![]() 是对角线
是对角线![]() 上一动点(不与
上一动点(不与![]() ,
,![]() 重合),连接
重合),连接![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,
,
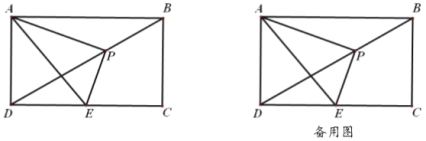
(1)求证:![]() ;
;
(2)当点![]() 是
是![]() 的中点时,求
的中点时,求![]() 的值;
的值;
(3)在点![]() 运动过程中,当
运动过程中,当![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人相约周末登花果山,甲、乙两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
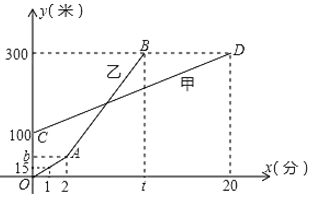
(1)甲登山上升的速度是每分钟 米,乙在A地时距地面的高度b为 米.
(2)若乙提速后,乙的登山上升速度是甲登山上升速度的3倍,请求出乙登山全程中,距地面的高度y(米)与登山时间x(分)之间的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某家具生产厂生产某种配套桌椅(一张桌子,两把椅子),已知每块板材可制作桌子![]() 张或椅子
张或椅子![]() 把,现计划用
把,现计划用![]() 块这种板材生产一批桌椅(不考虑板材的损耗,恰好配套),设用
块这种板材生产一批桌椅(不考虑板材的损耗,恰好配套),设用![]() 块板材做椅子,用
块板材做椅子,用![]() 块板材做桌子,则下列方程组正确的是( )
块板材做桌子,则下列方程组正确的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
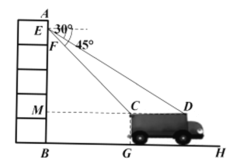
【题目】新冠状病毒疫情爆发,湖北武汉需要大量救援物资.如图小明站在一栋五层居民楼![]() 的第五层(每层高度相等),眼睛离五楼地面的距离
的第五层(每层高度相等),眼睛离五楼地面的距离![]() m.他发现楼外面停着一辆装载救援物资的货车,货车尾部C点到楼体的水平距离
m.他发现楼外面停着一辆装载救援物资的货车,货车尾部C点到楼体的水平距离![]() m,车箱顶部C点与地面的垂直距离
m,车箱顶部C点与地面的垂直距离![]() m;在E点测得C点的俯角为
m;在E点测得C点的俯角为![]() ,测得D点的俯角为
,测得D点的俯角为![]() ,求小明所在楼层
,求小明所在楼层![]() 的高度和货车车箱
的高度和货车车箱![]() 的长度(结果保留小数点后一位).
的长度(结果保留小数点后一位).
(参考数据:![]() ,
,![]() .)
.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(﹣1,0),与y轴的交点B在(0,﹣2)和(0,﹣1)之间(不包括这两点),对称轴为直线x=1.下列结论:①abc>0 ②4a+2b+c>0 ③4ac﹣b2<8a ④![]() <a<
<a<![]() ⑤b>c.其中含所有正确结论的选项是( )
⑤b>c.其中含所有正确结论的选项是( )

A. ①③ B. ①③④ C. ②④⑤ D. ①③④⑤
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com