
【题目】如图所示,以![]() 的边
的边![]() 为直径作
为直径作![]() ,点
,点![]() 在
在![]() 上,
上,![]() 是
是![]() 的弦,
的弦,![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() .
.
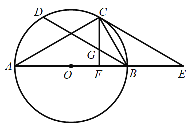
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)求证:![]() ;
;
(3)若![]() ,CG=4,求
,CG=4,求![]() 的长.
的长.
【答案】(1)证明见解析;(2)证明见解析;(3)![]()
【解析】
(1)连接OC,先证得![]() ,根据垂径定理得到OC⊥BD,根据CE//BD推出OC⊥CE,即可得到结论.
,根据垂径定理得到OC⊥BD,根据CE//BD推出OC⊥CE,即可得到结论.
(2)根据圆周角定理得出∠ACB=90°,然后根据同角的余角相等得出∠A=∠BCF,即可证得∠BCF=∠CBD,根据同角对等边即可证得结论.
(3)连接AD,根据圆周角定理得出∠ADB=90°,即可求得∠BAD=60°,根据圆周角定理得出∠DAC=∠BAC=30°,解直角三角形求得![]() ,然后根据三角形相似和等腰三角形的判定即可求得BE的值.
,然后根据三角形相似和等腰三角形的判定即可求得BE的值.
(1)连接OC
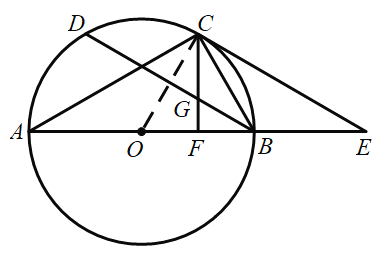
∵∠A=∠CBD
∴![]()
∴OC⊥BD
∵CE//BD
∴OC⊥CE
∴CE是⊙O的切线
(2)∵AB为直径
∴∠ACB=90°
∵CF⊥AB
∴∠ACB=∠CFB=90°
∵∠ABC=∠CBF
∴∠A=∠BCF
∵∠A=∠CBD
∴∠BCF=∠CBD
∴CG=BG
(3)连接AD,

∵AB为直径
∴∠ADB=90°
∵∠DBA=30°
∴∠BAD=60°
∵![]()
∴∠DAC=∠BAC=![]() ∠BAD=30°
∠BAD=30°
∴![]()
∵CE//BD,
∴∠E=∠DBA=30°
∴AC=CE,
∴![]()
∵∠BAC =∠BCF=∠CBD=30°
∴∠BCE=30°
∴BE=BC,
∴△CGB∽△CBE,
∴![]()
∵CG=4,
∴BC=![]()
∴BE=![]()
故答案为:![]()


科目:初中数学 来源: 题型:
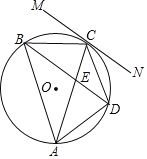
【题目】如图,⊙O为△ABC的外接圆,直线MN与⊙O相切于点C,弦BD∥MN,AC与BD相交于点E.
(1)求证:∠CAB=∠CBD;
(2)若BC=5,BD =8,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若△ABC绕点A逆时针旋转α后,与△ADE构成位似图形,则我们称△ABC与△ADE互为“旋转位似图形”.

(1)知识理解:
如图1,△ABC与△ADE互为“旋转位似图形”.
①若α=25°,∠D=100°,∠C=28°,则∠BAE= ;
②若AD=6,DE=7,AB=4,则BC=
(2)知识运用:
如图2,在四边形ABCD中,∠ADC=90°,AE⊥BD于点E,∠DAC=∠DBC,求证:△ACD与△ABE互为“旋转位似图形”.
(3)拓展提高:
如图3,△ABG为等边三角形,点C为AG的中点,点F是AB边上的一点,点D为CF延长线上的一点,点E在线段CF上,且△ABD与△ACE互为“旋转位似图形”.若AB=6,AD=4,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市特产大闸蟹,2016年的销售额是![]() 亿元,因生态优质美誉度高,销售额逐年增加2018年的销售额达
亿元,因生态优质美誉度高,销售额逐年增加2018年的销售额达![]() 亿元,若2017、2018年每年销售额增加的百分率都相同.
亿元,若2017、2018年每年销售额增加的百分率都相同.
(1)求平均每年销售额增加的百分率;
(2)该市这![]() 年大闸蟹的总销售额是多少亿元?
年大闸蟹的总销售额是多少亿元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,AB为
中,AB为![]() 的直径,C为
的直径,C为![]() 上一点,P是
上一点,P是![]() 的中点,过点P作AC的垂线,交AC的延长线于点D.
的中点,过点P作AC的垂线,交AC的延长线于点D.

(1)求证:DP是![]() 的切线;
的切线;
(2)若AC=5,![]() ,求AP的长.
,求AP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】教育局为了了解初一学生参加社会实践活动的天数,随机抽查本市部分初一学生参加社会实践活动的天数,并用得到的数据绘制了下面两幅不完整的统计图(如图).请你根据图中提供的信息,回答下列问题:
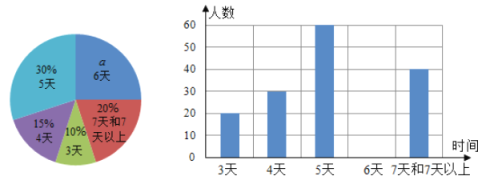
(1)这次共抽取 名学生进行统计调查,补全条形图;
(2)![]() ,该扇形所对圆心角的度数为 ;
,该扇形所对圆心角的度数为 ;
(3)如果该市有初一学生![]() 人,请你估计“活动时间不少于
人,请你估计“活动时间不少于![]() 天”的大约有多少人?
天”的大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,![]() 是
是![]() 的直径,弦
的直径,弦![]() 于G,过C点的切线与射线
于G,过C点的切线与射线![]() 相交于点E,直线
相交于点E,直线![]() 与
与![]() 交于点H,
交于点H,![]() ,
,![]() .
.

(Ⅰ)求![]() 的半径;
的半径;
(Ⅱ)将射线![]() 绕D点逆时针旋转,得射线
绕D点逆时针旋转,得射线![]() (如图2),
(如图2),![]() 与
与![]() 交于点M,与
交于点M,与![]() 及切线
及切线![]() 分别相交于点N,F,当
分别相交于点N,F,当![]() 时,求切线
时,求切线![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com