
【题目】若△ABC绕点A逆时针旋转α后,与△ADE构成位似图形,则我们称△ABC与△ADE互为“旋转位似图形”.

(1)知识理解:
如图1,△ABC与△ADE互为“旋转位似图形”.
①若α=25°,∠D=100°,∠C=28°,则∠BAE= ;
②若AD=6,DE=7,AB=4,则BC=
(2)知识运用:
如图2,在四边形ABCD中,∠ADC=90°,AE⊥BD于点E,∠DAC=∠DBC,求证:△ACD与△ABE互为“旋转位似图形”.
(3)拓展提高:
如图3,△ABG为等边三角形,点C为AG的中点,点F是AB边上的一点,点D为CF延长线上的一点,点E在线段CF上,且△ABD与△ACE互为“旋转位似图形”.若AB=6,AD=4,求![]() 的值.
的值.
【答案】(1)①27°;②![]() ;(2)见解析; (3)
;(2)见解析; (3)![]() .
.
【解析】
(1)①依据△ABC和△ADE互为“旋转位似图形”,可得△ABC∽△ADE,依据相似三角形的对应角相等,即可得到∠BAE=180°﹣100°﹣28°﹣25°=27°;
②依据△ABC∽△ADE,可得![]() ,根据AD=6,DE=7,AB=4,即可得出BC=
,根据AD=6,DE=7,AB=4,即可得出BC=![]() ;
;
(2)依据△AOD∽△BOC,即可得到![]() ,进而得到△AOB∽△DOC,再根据∠7=∠8,∠ADC=∠AEB,即可得到△ABE∽△ACD,进而得出△ACD和△ABE互为“旋转位似图形”;
,进而得到△AOB∽△DOC,再根据∠7=∠8,∠ADC=∠AEB,即可得到△ABE∽△ACD,进而得出△ACD和△ABE互为“旋转位似图形”;
(3)利用三角函数和勾股定理解答即可.
(1)①∵△ABC和△ADE互为“旋转位似图形”,
∴△ABC∽△ADE,
∴∠D=∠B=100°,
又∵α=25°,∠E=28°,
∴∠BAE=180°﹣100°﹣25°﹣28°=27°;
②∵△ABC∽△ADE,
∴![]() ,
,
∵AD=6,DE=7,AB=4,
∴![]() ,
,
∴BC=![]() ,
,
故答案为:27°;![]() ;
;
(2)∵∠DOA=∠COB,∠DAC=∠DBC,
∴△DOA∽△COB,
∴![]() ,即
,即![]() ,
,
又∵∠DOC=∠AOB,
∴△AOB∽△DOC,
∴∠DCA=∠EBA,
又∵∠ADC=90°,AE⊥BD,
∴∠ADC=∠AEB=90°,
∴△ABE∽△ACD,
∴∠DAC=∠EAB,
∴△AEB绕点A逆时针旋转∠DAE的度数后与△ADC构成位似图形,
∴△ACD和△ABE互为“旋转位似图形”;
(3)∵AC=![]() AG=
AG=![]() AB=3,
AB=3,
由题意得:![]() ,
,
∵AD=4,
∴AE=2,
∵∠DAE=∠FAC=60°,
∴cos∠DAE=cos60°=![]() ,
,
∴∠DEA=90°,
∴由勾股定理可得CE=![]() ,
,
∴DE=AEtan∠DAE=2![]() ,
,
∴![]() .
.


 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案科目:初中数学 来源: 题型:
【题目】某商场用24 000元购入一批空调,然后以每台3 000元的价格销售,因天气炎热.空调很快售完;商场又用52 000元再次购入一批该种型号的空调,数量是第一次购入的2倍,但购入的单价上调了200元,每台的售价也上调了200元.
(1)商场第一次购入的空调每台进价是多少元?
(2)商场既要尽快售完第二次购入的空调,又要在第二次空调销售中获得的利润率不低于20%,打算将第二次购入的部分空调按每台九五折出售,最多可将多少台空调打折出售?
查看答案和解析>>
科目:初中数学 来源: 题型:
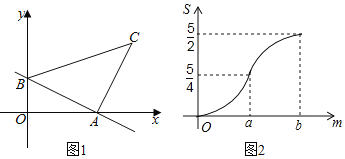
【题目】如图1,直线AB与x轴、y轴分别相交于点A、B,将线段AB绕点A顺时针旋转90°,得到AC,连接BC,将△ABC沿射线BA平移,当点C到达x轴时运动停止.设平移距离为m,平移后的图形在x轴下方部分的面积为S,S关于m的函数图象如图2所示(其中0<m≤a,a<m≤b时,函数的解析式不同).
(1)填空:△ABC的面积为 ;
(2)求直线AB的解析式;
(3)求S关于m的解析式,并写出m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点![]() (顶点是网格线的交点)和直线l及点O.
(顶点是网格线的交点)和直线l及点O.
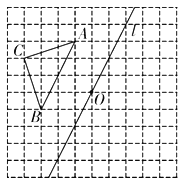
(1)画出![]() 关于直线l对称的
关于直线l对称的![]() ;
;
(2)连接OA,将OA绕点O顺时针旋转![]() ,画出旋转后的线段;
,画出旋转后的线段;
(3)在旋转过程中,当OA与![]() 有交点时,旋转角
有交点时,旋转角![]() 的取值范围为________.
的取值范围为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
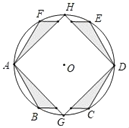
【题目】如图,在半径为6的⊙O中,正六边形ABCDEF与正方形AGDH都内接于⊙O,则图中阴影部分的面积为( )
A. 27﹣9![]() B. 18
B. 18![]() C. 54﹣18
C. 54﹣18![]() D. 54
D. 54
查看答案和解析>>
科目:初中数学 来源: 题型:
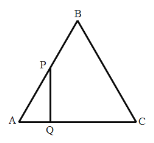
【题目】如图等边![]() 的边长为
的边长为![]() ,点
,点![]() ,点
,点![]() 同时从点
同时从点![]() 出发,点
出发,点![]() 沿
沿![]() 以
以![]() 的速度向点
的速度向点![]() 运动,点
运动,点![]() 沿
沿![]() 以
以![]() 的速度也向点
的速度也向点![]() 运动,直到到达点
运动,直到到达点![]() 时两点都停止运动,若
时两点都停止运动,若![]() 的面积为
的面积为![]() ,点
,点![]() 的运动时间为
的运动时间为![]() ,则下列最能反映
,则下列最能反映![]() 与
与![]() 之间函数关系的图象是( )
之间函数关系的图象是( )
A.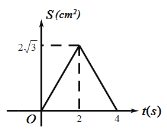 B.
B.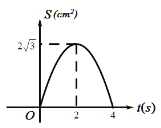
C.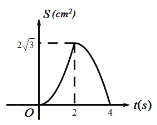 D.
D.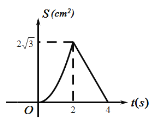
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,以![]() 的边
的边![]() 为直径作
为直径作![]() ,点
,点![]() 在
在![]() 上,
上,![]() 是
是![]() 的弦,
的弦,![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() .
.
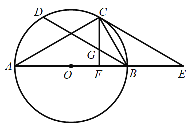
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)求证:![]() ;
;
(3)若![]() ,CG=4,求
,CG=4,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人相约周末登花果山,甲、乙两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
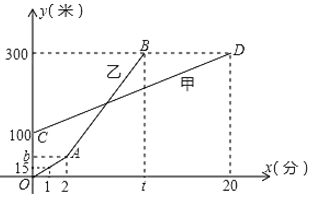
(1)甲登山上升的速度是每分钟 米,乙在A地时距地面的高度b为 米.
(2)若乙提速后,乙的登山上升速度是甲登山上升速度的3倍,请求出乙登山全程中,距地面的高度y(米)与登山时间x(分)之间的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为丰富学生的校园生活,准备从体育用品商店一次性购买若干个足球和篮球(每个足球的价格相同,每个篮球的价格相同),若购买3个足球和2个篮球共需310元,购买2个足球和5个篮球共需500元。
(1)求购买一个足球、一个篮球各需多少元?
(2)根据学校实际情况,需从体育用品商店一次性购买足球和篮球共96个,要求购买足球和篮球的总费用不超过5720元,这所中学最多可以购买多少个篮球?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com