
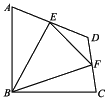
【题目】如图,在四边形ABCD中,∠ABC=90°,AB=BC=2![]() ,E,F分别是AD,CD的中点,连结BE,BF,EF.若四边形ABCD的面积为6,则△BEF的面积为( )
,E,F分别是AD,CD的中点,连结BE,BF,EF.若四边形ABCD的面积为6,则△BEF的面积为( )
A. 2B. ![]() C.
C. ![]() D. 3
D. 3
【答案】C
【解析】
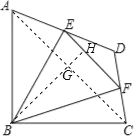
连接AC,过B作EF的垂线,利用勾股定理可得AC,易知△ABC的面积,可得BG和△ADC的面积,三角形ABC与三角形ACD同底,利用面积比可得出他们的高之比,而GH又是△ACD以AC为底的高的一半,可得GH,易得BH,由中位线的性质可得EF的长,利用三角形的面积公式可得结果.
连接AC,过B点作EF的垂线交AC于点G,交EF于点H,
∵EF∥AC
∴BG⊥AC
∵∠ABC=90°,AB=BC=2![]() ,
,
∴AC=![]() =4,
=4,
∵△ABC为等腰三角形
∴△ABG,△BCG为等腰直角三角形,
∴AG=BG=2,
∵S△ABC=![]() ·AB·BC=
·AB·BC=![]() 2
2![]() 2
2![]() =4,
=4,
∴S△ACD=2,
∵![]() =2,
=2,
∴GH=![]() BG=
BG=![]() ,
,
∴BH=![]() ,
,
又∵EF=![]() AC=2,
AC=2,
∴S△BEF=![]() ·EF·BH=
·EF·BH=![]() 2
2![]() =
=![]() .
.
故选C.


 学习实践园地系列答案
学习实践园地系列答案科目:初中数学 来源: 题型:
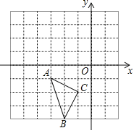
【题目】如图,在直角坐标系中,每个小方格都是边长为![]() 的正方形,
的正方形,![]() 的顶点均在格点上,点
的顶点均在格点上,点![]() 的坐标是
的坐标是![]() .
.
![]() 先将
先将![]() 沿
沿![]() 轴正方向向上平移
轴正方向向上平移![]() 个单位长度,再沿
个单位长度,再沿![]() 轴负方向向左平移
轴负方向向左平移![]() 个单位长度得到
个单位长度得到![]() ,画出
,画出![]() ,点
,点![]() 坐标是________;
坐标是________;
![]() 将
将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() ,得到
,得到![]() ,画出
,画出![]() ,并求出点
,并求出点![]() 的坐标是________;
的坐标是________;
![]() 我们发现点
我们发现点![]() 、
、![]() 关于某点中心对称,对称中心的坐标是________.
关于某点中心对称,对称中心的坐标是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数学课上,老师提出一个问题“用直尺和圆规作以AB为底的等腰直角三角形ABC”.
小美的作法如下:
①分别以点A,B为圆心,大于![]() AB作弧,交于点M,N;
AB作弧,交于点M,N;
②作直线MN,交AB于点O;
③以点O为圆心,OA为半径,作半圆,交直线MN于点C;
④连结AC,BC.
所以,△ABC即为所求作的等腰直角三角形.
请根据小美的作法,用直尺和圆规作以AB为底的等腰直角三角形ABC,并保留作图痕迹.这种作法的依据是 .
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表中有两种移动电话计费方式:

说明:月使用费固定收取,主叫不超限定时间不再收费,主叫超时部分加收超时费,被叫免费.
(1)若李明某月主叫通话时间为700分钟,则他按方式一计费需 元,按方式二计费需 元(用含![]() 的代数式表示);若他按方式一计费需60元,则主叫通话时间为 分钟;
的代数式表示);若他按方式一计费需60元,则主叫通话时间为 分钟;
(2)若方式二中主叫超时费![]() (元/分钟),是否存在某主叫通话时间
(元/分钟),是否存在某主叫通话时间![]() (分钟),按方式一和方式二的计费相等?若存在,请求出
(分钟),按方式一和方式二的计费相等?若存在,请求出![]() 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;
(3)若主叫时间为750分钟时,两种方式的计费相等,直接写出![]() 的值为 ;请你通过计算分析后,直接给出当月主叫通话时间
的值为 ;请你通过计算分析后,直接给出当月主叫通话时间![]() (分钟)满足什么条件时,选择方式二省钱?
(分钟)满足什么条件时,选择方式二省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中学初三(1)班共有40名同学,在一次30秒跳绳测试中他们的成绩统计如下表:
跳绳数/个 | 81 | 85 | 90 | 93 | 95 | 98 | 100 |
人 数 | 1 | 2 | 8 | 11 | 5 |
将这些数据按组距5(个)分组,绘制成如图的频数分布直方图(不完整).
(1)将表中空缺的数据填写完整,并补全频数分布直方图;
(2)这个班同学这次跳绳成绩的众数是 个,中位数是 个;
(3)若跳满90个可得满分,学校初三年级共有720人,试估计该中学初三年级还有多少人跳绳不能得满分.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
小明遇到这样一个问题:如图1,在边长为![]() 的正方形ABCD各边上分别截取AE=BF=CG=DH=1,当∠AFQ=∠BGM=∠CHN=∠DEP=45°时,求正方形MNPQ的面积。
的正方形ABCD各边上分别截取AE=BF=CG=DH=1,当∠AFQ=∠BGM=∠CHN=∠DEP=45°时,求正方形MNPQ的面积。
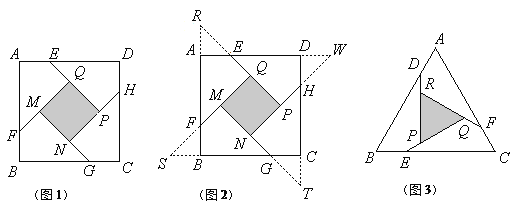
小明发现:分别延长QE、MF、NG、PH交FA、GB、HC、ED的延长线于点R、S、T、W可得△RQF、△SMG、△TNH、△WPE是四个全等的等腰直角三角形(如图2)
请回答:
(1)若将上述四个等腰直角三角形拼成一个新的正方形(无缝隙,不重叠),则这个新的正方形的边长为__________;
(2)求正方形MNPQ的面积.
参考小明思考问题的方法,解决问题:
如图3,在等边△ABC各边上分别截取AD=BE=CF,再分别过点D、E、F作BC、AC、AB的垂线,得到等边△RPQ,若![]() ,则AD的长为__________.
,则AD的长为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
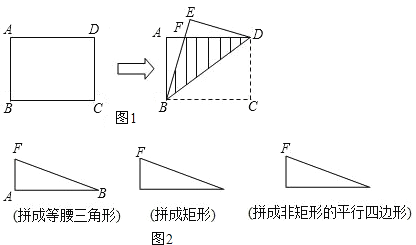
【题目】已知:如图1,把一张矩形纸片ABCD沿对角线BD折叠,将重合部分(△BFD)剪去,得到△ABF和△EDF.
(1)求证:FB=FD;
(2)求证:△ABF≌△EDF;
(3)将△ABF与△EDF不重合地拼在一起,可拼成特殊三角形和特殊四边形,请你按照下列要求将拼图补画完整(图2).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ACB与△ECD都是等腰直角三角形,∠ACB=∠ECD=90,点D为AB边上的一点,

(1)试说明:∠EAC=∠B ;
(2)若AD=15,BD=36,求DE的长.
(3)若点D在A、B之间移动,当点D为 时,AC与DE互相平分.
(直接写出答案,不必说明理由)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据下列语句,画出图形.
(1)如图1,已知![]() 四点.
四点.
①画直线![]() ;
;
②连接线段![]() ,相交于点
,相交于点![]() ;
;
③画射线![]() ,相交于点
,相交于点![]() .
.
(2)如图2,有一个灯塔分别位于海岛![]() 的南偏西30°和海岛
的南偏西30°和海岛![]() 的南偏西60°的方向上,通过画图可推断灯塔的位置可能是
的南偏西60°的方向上,通过画图可推断灯塔的位置可能是![]() 四点中的____点.
四点中的____点.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com