

分析 (1)设正方形ABCD的边长为1,则BD=$\sqrt{2}$,由折叠性质可知BG=BC=1,∠AFE=∠BFE=90°,则四边形BCEF为矩形,得出EF∥AD,由平行线分线段成比例得出$\frac{BG}{BD}$=$\frac{BF}{AB}$,求出BF=$\frac{1}{\sqrt{2}}$,则BC:BF=1:$\frac{1}{\sqrt{2}}$=$\sqrt{2}$:1,即四边形BCEF为$\sqrt{2}$矩形;
(2)(Ⅰ)在Rt△BFG中,由勾股定理得:FG=$\sqrt{B{G}^{2}-B{F}^{2}}$,即可解得$\frac{AD}{FG}$;
(Ⅱ)由勾股定理解得BE=$\sqrt{E{C}^{2}+B{C}^{2}}$,由折叠可得BP=BC=1,∠FNM=∠BNM=90°,∠EMN=∠CMN=90°,证得四边形BCMN是矩形,得出MN∥EF,由平行线分线段成比例得出$\frac{BP}{BE}$=$\frac{BN}{BF}$,求得BN=$\frac{1}{\sqrt{3}}$,则BC:BN=1:$\frac{1}{\sqrt{3}}$=$\sqrt{3}$:1,即四边形BCMN是$\sqrt{3}$的矩形,即可得出结果.
解答 (1)证明:设正方形ABCD的边长为1,则BD=$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$,
由折叠性质可知BG=BC=1,∠AFE=∠BFE=90°,则四边形BCEF为矩形,
∴∠A=∠BFE,
∴EF∥AD,
∴$\frac{BG}{BD}$=$\frac{BF}{AB}$,即:$\frac{1}{\sqrt{2}}$=$\frac{BF}{1}$,
∴BF=$\frac{1}{\sqrt{2}}$,
∴BC:BF=1:$\frac{1}{\sqrt{2}}$=$\sqrt{2}$:1,
∴四边形BCEF为$\sqrt{2}$矩形;
(2)解:(Ⅰ)在Rt△BFG中,由勾股定理得:FG=$\sqrt{B{G}^{2}-B{F}^{2}}$=$\sqrt{{1}^{2}-(\frac{1}{\sqrt{2}})^{2}}$=$\sqrt{\frac{1}{2}}$=$\frac{\sqrt{2}}{2}$,
∴$\frac{AD}{FG}$=$\frac{1}{\frac{\sqrt{2}}{2}}$=$\sqrt{2}$;
(Ⅱ)∵BC=1,EC=BF=$\frac{1}{\sqrt{2}}$,
∴BE=$\sqrt{E{C}^{2}+B{C}^{2}}$=$\sqrt{(\frac{1}{\sqrt{2}})^{2}+{1}^{2}}$=$\sqrt{\frac{3}{2}}$=$\frac{\sqrt{6}}{2}$,
由折叠可得BP=BC=1,∠FNM=∠BNM=90°,∠EMN=∠CMN=90°.
∵四边形BCEF是矩形,
∴∠F=∠FEC=∠C=∠FBC=90°,
∴四边形BCMN是矩形,∠BNM=∠F=90°,
∴MN∥EF,
∴$\frac{BP}{BE}$=$\frac{BN}{BF}$,即BP•BF=BE•BN,
∴1×$\frac{1}{\sqrt{2}}$=$\frac{\sqrt{6}}{2}$BN,
∴BN=$\frac{1}{\sqrt{3}}$,
∴BC:BN=1:$\frac{1}{\sqrt{3}}$=$\sqrt{3}$:1,
∴四边形BCMN是$\sqrt{3}$的矩形,
∴n=3.
故答案为:$\sqrt{2}$;3.
点评 本题主要考查了折叠的性质、正方形的性质、矩形的判定与性质、平行线分线段成比例、勾股定理等知识;熟练掌握折叠的性质是解决问题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
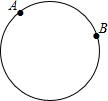 如图,已知一周长为30cm的圆形轨道上有相距10cm的A、B两点(备注:圆形轨道上两点间的距离是指圆上这两点间的较短部分展直后的线段长).动点P从A点出发,以acm/s的速度,在轨道上逆时针方向运动,与此同时,动点Q从B点出发,以3cm/s的速度,按同样的方向运动,设运动时间为t(s),当t=5时,动点P、Q第一次相遇.
如图,已知一周长为30cm的圆形轨道上有相距10cm的A、B两点(备注:圆形轨道上两点间的距离是指圆上这两点间的较短部分展直后的线段长).动点P从A点出发,以acm/s的速度,在轨道上逆时针方向运动,与此同时,动点Q从B点出发,以3cm/s的速度,按同样的方向运动,设运动时间为t(s),当t=5时,动点P、Q第一次相遇.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在平面直角坐标系xOy中,抛物线y=ax2-3ax+c与x轴交于A(-1,0)、B两点(A点在B点左侧),与y轴交于点C(0,2).
在平面直角坐标系xOy中,抛物线y=ax2-3ax+c与x轴交于A(-1,0)、B两点(A点在B点左侧),与y轴交于点C(0,2).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com