
【题目】在等边三角形ABC,点D在BC上,点E在AG的延长线上,DE=DA(如图1).

(1)求证:∠BAD=∠EDC;
(2)如图2,若点E关于直线BC的对称点为M,连DM,AM,请判断△ADM的形状,并说明理由.
【答案】(1)见解析;(2)△ADM是等边三角形,理由见解析.
【解析】
(1)根据等腰三角形的性质,得出∠E=∠DAC,根据等边三角形的性质,得出∠BAD+∠DAC=∠E+∠EDC=60°,据此可得出∠BAD=∠EDC;
(2)月轴对称的性质得出DE=DM,∠DEC=∠MDC,进而证得△ADM是等腰三角形,∠BAD=∠CDM,根据三角形外角的性质即可证得∠ADM=60°,从而证得△ADM是等边三角形.
(1)证明:∵△ABC是等边三角形
∴∠BAC=∠ACB=∠B=60°
又∵∠BAC=∠BAD+∠DAC
∠ACB=∠E+∠EDC
又∵DE=DA
∴∠BAD=∠EDC;
(2)解:△ADM是等边三角形,
理由:∵点E、M关于直线BC对称
∴DE=DM,∠DEC=∠MDC
又∵DE=DA
∴DM=DA
∴△ADM是等腰三角形
又∵∠BAD=∠EDC
∴∠BAD=∠MDC
又∵∠ADM+∠MDC=∠B+∠BAD
∴∠ADM=∠B=60°
∴△ADM是等边三角形.


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案科目:初中数学 来源: 题型:
【题目】若a、b、c是△ABC中∠A、∠B、∠C的对边,抛物线y=x2﹣2ax+b2交x轴于M(a+c,0),则△ABC是( )
A. 等腰三角形 B. 等边三角形 C. 直角三角形 D. 不确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,AB=AC,BO、CO 分别平分∠ABC、∠ACB,DE 经过点 O, 且 DE∥BC,DE 分别交 AB、AC 于 D、E,则图中等腰三角形的个数为( )

A.2B.3C.4D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点A(1,n1),点B(2,n2)在一次函数y1=k1x+b1图像上:点C(3,n3),点D(4,n4)在一次函数y2=k2x+b2图像上,y1 和y2图像交点坐标是(m,n).若n4<n1<n3<n2,则下列说法:①k1>0,k2<0;②k1<0,k2>0;③1<m<3;④2<m<4,正确的是____(填序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠C=72°,∠B=∠D=90°,E,F分别是DC,BC上的点,当△AEF的周长最小时,∠EAF的度数为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是长为10m,倾斜角为37°的自动扶梯,平台BD与大楼CE垂直,且与扶梯AB的长度相等,在B处测得大楼顶部C的仰角为65°,求大楼CE的高度(结果保留整数).
(参考数据:sin37°≈![]() ,tan37°≈
,tan37°≈![]() ,sin65°≈
,sin65°≈![]() ,tan65°≈
,tan65°≈![]() )
)
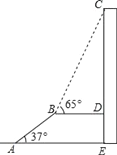
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是△ABC的中线,E,F分别是AD和AD延长线上的点,且DE=DF,连结BF,CE.下列说法①△BDF≌△CDE;②△ABD和△ACD面积相等;③BF∥CE;④CE=BF.其中正确的有( )

A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠ABC=20°,点D,E分别在射线BC,BA上,且BD=3,BE=3,点M,N分别是射线BA,BC上的动点,求DM+MN+NE的最小值为_____.
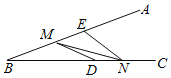
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料,完成相应任务:



(1)小明在研究命题①时,在图1的正方形网格中画出两个符合条件的四边形.由此判断命题①是 命题(填“真”或“假”).
(2)小彬经过探究发现命题②是真命题.请你结合图2证明这一命题.
(3)小颖经过探究又提出了一个新的命题:“若![]() ,
,![]() ,
,![]() , , ,则四边形
, , ,则四边形![]() ≌四边形
≌四边形![]() ”请在横线上填写两个关于“角”的条件,使该命题为真命题.
”请在横线上填写两个关于“角”的条件,使该命题为真命题.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com