
 已知:抛物线C1:y=2x2+bx+6与抛物线C2关于y轴对称,抛物线C1与x轴分别交于点A(-3,0),B(m,0),顶点为M.
已知:抛物线C1:y=2x2+bx+6与抛物线C2关于y轴对称,抛物线C1与x轴分别交于点A(-3,0),B(m,0),顶点为M.分析 (1)把A(-3,0)代入y=2x2+bx+6,即可求得b的值,从而求得解析式,令y=0,j解方程即可求得m的值;
(2)根据C1:y=2x2+8x+6=2(x+2)2-2,求得顶点M(-2,-2),即可求得点M关于y轴的对称点N(2,-2),由于a的值不变,根据顶点得出C2:y=2(x-2)2-2=2x2-8x+6;
(3)根据P、Q的坐标求得直线PQ的解析式,然后分三种情况讨论求得.
解答 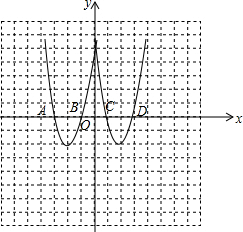 解:(1)∵抛物线y=2x2+bx+6过点 A(-3,0),
解:(1)∵抛物线y=2x2+bx+6过点 A(-3,0),
∴0=18-3b+6,
∴b=8,
∴C1:y=2x2+8x+6,
令y=0,则2x2+8x+6=0,
解得x1=-3,x2=-1
∴m=-1;
(2)∵C1:y=2x2+8x+6=2(x+2)2-2,
∴M(-2,-2),
∴点M关于y轴的对称点N(2,-2),
∴C2:y=2(x-2)2-2=2x2-8x+6,
(3)由题意,点A(-3,0)与D,点B(-1,0)与C关于y轴对称,
∴D(3,0),C(1,0),
∵P(t,0),Q(0,-2t),
∴PQ:y=2x-2t,
当PQ过点C时,即P与C重合时,t=1,
当PQ过点D时,即P与D重合时,t=3,
当直线PQ与抛物线C2有且仅有一个公共点时,即方程2x2-8x+6=2x-2t中△=0,
方程整理得x2-5x+3+t=0,△=25-4(3+t)=0,
解得t=$\frac{13}{4}$.
综上,由图得,当1≤t<3或t=$\frac{13}{4}$时,PQ与抛物线C2有且仅有一个公共点.
点评 本题主要考查抛物线与x轴的交点,二次函数与几何变换,解一元二次方程,综合运用这些性质进行推理是解此题的关键,题目比较典型,难度适中.


 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:初中数学 来源: 题型:解答题
 如图是边长为1的小正方形组成的格点图,坐标轴的单位长度为1,根据要求解答下列问题:
如图是边长为1的小正方形组成的格点图,坐标轴的单位长度为1,根据要求解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知抛物线y=-2x2+4x-1.
已知抛物线y=-2x2+4x-1.| x | … | … | |||||
| y | … | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
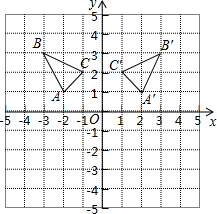 如图是一个的正方形格纸,△ABC中A点坐标为(-2,1).
如图是一个的正方形格纸,△ABC中A点坐标为(-2,1).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 28.30千克 | B. | 27.70千克 | C. | 28.51千克 | D. | 27.80千克 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com