Question

14．如图，在平面直角坐标系中，⊙Q交坐标轴于A，B，C，D，点P在弦EB的延长线上，且BC平分∠ABP．
（1）求证：$\widehat{AC}$=$\widehat{EC}$；
（2）若点B的坐标是（2，0），求AB-BE的值．

Answer 1

分析 （1）首先连接AC，CE，由圆的内接四边形的性质，易得∠PBC=∠EAC，又由BC平分∠ABP，可得∠EAC=∠ABC，即可证得$\widehat{AC}$=$\widehat{EC}$；
（2）首先连接CE，在AB上取点G，使得AG=BE，连接CG，易证得△ACG≌△ECB（SAS），然后证得△BCG是等腰三角形，即可求得BG的长，继而求得答案．

解答 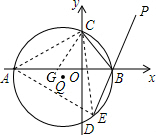（1）证明：连接AC，AE，
∵四边形ABCD内接于⊙Q，
∴∠CBE+∠CAE=180°，
∵∠PBC+∠CBE=180°，
∴∠PBC=∠CAE，
又∵BC平分∠ABP，
∴∠ABC=∠PBC，
∴∠ABC=∠CAE，
∴$\widehat{AC}$=$\widehat{EC}$；

（2）解：连接CE，在AB上取点G，使得AG=BE，连接CG，
∵B（2，0），
∴OB=2，
∵$\widehat{AC}$=$\widehat{EC}$，
∴AC=CE，
在△ACG和△ECB中，
$\left\{\begin{array}{l}{AC=CE}\\{∠BAC=∠BEC}\\{AG=EB}\end{array}\right.$，
∴△ACG≌△ECB（SAS），
∴CG=CB，
又∵DC⊥AB，
∴OG=OB=2，
∴BG=2OB=4，
∴AB-BE=AB-AG=BG=4．

点评 此题属于圆的综合题，考查了圆周角的性质、圆的内接四边形的性质、全等三角形的判定与性质以及弧与弦的关系．注意准确作出辅助线是解此题的关键．