
 如图,在矩形ABCD中,AB=12cm,BC=6cm,点P沿AB边从点A开始向点B以2cm/s的速度移动,点Q沿DA边从点D开始向点A以1cm/s的速度移动,如果P、Q同时出发,用t表示移动的时间(0≤t≤6),那么:
如图,在矩形ABCD中,AB=12cm,BC=6cm,点P沿AB边从点A开始向点B以2cm/s的速度移动,点Q沿DA边从点D开始向点A以1cm/s的速度移动,如果P、Q同时出发,用t表示移动的时间(0≤t≤6),那么:分析 (1)根据题意得到AP=2t,DQ=t,根据等腰直角三角形的性质列出方程,解方程即可;
(2)根据四边形QAPC的面积=四边形ABCD的面积-△CDQ的面积-△PBC的面积计算;
(3)用t表示出△PCQ的面积,根据题意列出一元二次方程,解方程即可.
解答 解:(1)由题意得,AP=2t,DQ=t,
则PB=12-2t,AQ=6-t,
△QAP是等腰直角三角形,
则AQ=AP,即6-t=2t,
解得,t=2,
答:当t=2时,△QAP是等腰直角三角形;
(2)四边形QAPC的面积=四边形ABCD的面积-△CDQ的面积-△PBC的面积
=12×6-$\frac{1}{2}$×12×t-$\frac{1}{2}$×6×(12-2t)
=36;
(3)△PCQ的面积=四边形QAPC的面积-△QAP的面积
=36-$\frac{1}{2}$×2t×(6-t)
=36-6t+t2,
当△PCQ的面积是31cm2时,36-6t+t2=31,
解得,t1=1,t2=5,
则当t=1或5时,△PCQ的面积是31cm2.
点评 本题考查的是矩形的性质、等腰直角三角形的性质以及一元二次方程的解法,根据题意正确表示出线段AP、DQ的长度、灵活运用相关的性质定理列出关系式是解题的关键.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,⊙Q交坐标轴于A,B,C,D,点P在弦EB的延长线上,且BC平分∠ABP.
如图,在平面直角坐标系中,⊙Q交坐标轴于A,B,C,D,点P在弦EB的延长线上,且BC平分∠ABP.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知一次函数y1=2x-3与y2=-x+4的图象相交于点P,它们与y轴交于A、B两点.
已知一次函数y1=2x-3与y2=-x+4的图象相交于点P,它们与y轴交于A、B两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
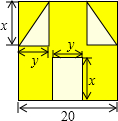 “囧”像一个人脸郁闷的神情.如图,边长为a的正方形纸片,剪去两个一样的小直角三角形和一个长方形得到一个“囧”字图案(阴影部分),设剪去的两个小直角三角形的两直角边长分别为x、y,剪去的小长方形长和宽也分别为x,y.
“囧”像一个人脸郁闷的神情.如图,边长为a的正方形纸片,剪去两个一样的小直角三角形和一个长方形得到一个“囧”字图案(阴影部分),设剪去的两个小直角三角形的两直角边长分别为x、y,剪去的小长方形长和宽也分别为x,y.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 +(-3x2+5x-7)=-2x2+3x-6
+(-3x2+5x-7)=-2x2+3x-6查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在斜坡的顶部有一铁塔AB,B是CD的中点,CD是水平的,在阳光的照射下,塔影DE留在坡面上.已知CD=12m,DE=18m,小明和小华的身高都是1.5m,同一时刻小明站在E处,影子落在坡面上,影长为2m,小华站在平地上,影子也落在平地上,影长为1m,则塔高AB是22.5米.
如图,在斜坡的顶部有一铁塔AB,B是CD的中点,CD是水平的,在阳光的照射下,塔影DE留在坡面上.已知CD=12m,DE=18m,小明和小华的身高都是1.5m,同一时刻小明站在E处,影子落在坡面上,影长为2m,小华站在平地上,影子也落在平地上,影长为1m,则塔高AB是22.5米.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com