
 问题情境:我们知道,两边及其中一边所对的角分别对应相等的两个三角形不一定全等,那么在什么情况下,这样的两个三角形才全等呢?为了研究这个问题,我们先思考下面几个问题:
问题情境:我们知道,两边及其中一边所对的角分别对应相等的两个三角形不一定全等,那么在什么情况下,这样的两个三角形才全等呢?为了研究这个问题,我们先思考下面几个问题:分析 (1)根据作图要求结合画图过程作图即可,作出的B点位置不是一个;
(2)过C作CD⊥AN,利用直角三角形的性质可得CD长,再根据勾股定理计算出AD长和BD长,即可得答案;
(3)添加三角形的形状要求,便可作出唯一的三角形.
解答  解:(1)作法:①∠MAN=∠a;
解:(1)作法:①∠MAN=∠a;
②在射线AM上截取线段AC=b;
③以C为圆心、a长为半径画弧交射线AN于点B;
④连接BC,则△ACB就是所求作的三角形.
(2)过C作CD⊥AN,
∵∠α=30°,b=8,
∴CD=$\frac{1}{2}$AC=4,
∴AD=$\sqrt{A{C}^{2}-C{D}^{2}}$=$\sqrt{64-16}$=4$\sqrt{3}$,
∵a=5,
∴CB=5,
∴BD=$\sqrt{C{B}^{2}-C{D}^{2}}$=$\sqrt{25-16}$=3,
∴AB=4$\sqrt{3}$+3或4$\sqrt{3}$-3;
(3)再增加三角形为锐角三角形,或三角形为直角三角形,或添加三角形为钝角三角形的条件,三角形的形状便可以确定,便可判定两个三角形全等.
点评 此题主要考查了复杂作图,以及勾股定理的应用,关键是正确根据作图要求画出图形,掌握直角三角形两直角边的平方和等于斜边的平方.


科目:初中数学 来源: 题型:填空题
 如图,线段CD两个端点的坐标分别为C(1,2)、D(2,0),以原点为位似中心,将线段CD放大得到线段AB,若点B的坐标为(5,0),则点A的坐标为(2.5,5).
如图,线段CD两个端点的坐标分别为C(1,2)、D(2,0),以原点为位似中心,将线段CD放大得到线段AB,若点B的坐标为(5,0),则点A的坐标为(2.5,5).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,点A的纵坐标为2,点B在x轴的负半轴上,AB=AO,∠ABO=30°,直线MN经过原点O,点A关于直线MN的对称点A1在x轴的正半轴上.
如图,在平面直角坐标系中,点A的纵坐标为2,点B在x轴的负半轴上,AB=AO,∠ABO=30°,直线MN经过原点O,点A关于直线MN的对称点A1在x轴的正半轴上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,正方形ABCD的边长为6cm,E为CD边上一点,∠DAE=30°,M为AE的中点,过点M作直线分别与AD、BC相交于点P、Q.若PQ=AE,则AP等于2或4cm.
如图,正方形ABCD的边长为6cm,E为CD边上一点,∠DAE=30°,M为AE的中点,过点M作直线分别与AD、BC相交于点P、Q.若PQ=AE,则AP等于2或4cm.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,Rt△ABC中,∠C=90°,AC=3,BC=4,点D在AB边上,点E是BC边上一点(不与点B、C重合),且DA=DE,则AD的取值范围是( )
如图,Rt△ABC中,∠C=90°,AC=3,BC=4,点D在AB边上,点E是BC边上一点(不与点B、C重合),且DA=DE,则AD的取值范围是( )| A. | 0<AD<3 | B. | 1≤AD<$\frac{5}{2}$ | C. | $\frac{15}{7}$≤AD<$\frac{5}{2}$ | D. | $\frac{15}{8}$≤AD<$\frac{5}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,⊙Q交坐标轴于A,B,C,D,点P在弦EB的延长线上,且BC平分∠ABP.
如图,在平面直角坐标系中,⊙Q交坐标轴于A,B,C,D,点P在弦EB的延长线上,且BC平分∠ABP.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
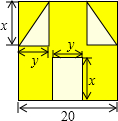 “囧”像一个人脸郁闷的神情.如图,边长为a的正方形纸片,剪去两个一样的小直角三角形和一个长方形得到一个“囧”字图案(阴影部分),设剪去的两个小直角三角形的两直角边长分别为x、y,剪去的小长方形长和宽也分别为x,y.
“囧”像一个人脸郁闷的神情.如图,边长为a的正方形纸片,剪去两个一样的小直角三角形和一个长方形得到一个“囧”字图案(阴影部分),设剪去的两个小直角三角形的两直角边长分别为x、y,剪去的小长方形长和宽也分别为x,y.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com