Question

10．如图，在平面直角坐标系中，点A的纵坐标为2，点B在x轴的负半轴上，AB=AO，∠ABO=30°，直线MN经过原点O，点A关于直线MN的对称点A₁在x轴的正半轴上．
（1）求点B关于直线MN的对称点B₁的横坐标；
（2）求证：AB+BO=AB₁．

Answer 1

分析 （1）过A作AC⊥x轴于C，过B作BD⊥x轴于D，根据点A的纵坐标为1求出AO=2，OC=2$\sqrt{3}$，BO=4$\sqrt{3}$=OB₁，根据∠B₁DO=90°和∠DOB₁=30°求出OD即可；
（2）根据轴对称得出线段AB₁线段A₁B关于直线MN对称，求出AB₁=A₁B，根据A₁B=A₁O+BO和A₁O=AO推出即可．

解答 解：（1）如图，过A作AC⊥x轴于C，过B₁作BD⊥x轴于D，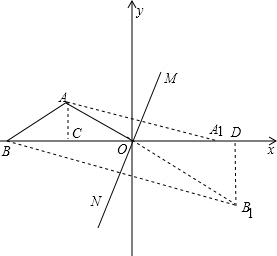

∵点A的纵坐标为2，
∴AC=2，
∵AB=AO，∠ABO=30°，
∴AO=2，OC=2$\sqrt{3}$，BO=4$\sqrt{3}$=OB₁，
∵∠B₁DO=90°，∠DOB₁=30°，
∴B₁D=$\sqrt{3}$，OD=2$\sqrt{3}$B₁D=6，
∴点B关于直线MN的对称点B₁的横坐标3；
（2）∵A关于直线MN的对称点A₁在x轴的正半轴上，点B关于直线MN的对称点为B₁，
∴线段AB₁线段A₁B关于直线MN对称，
∴AB₁=A₁B，
而A₁B=A₁O+BO，A₁O=AO，
∴AB₁=AO+BO．

点评 本题考查了含30度角的直角三角形性质，轴对称性质，线段垂直平分线性质，勾股定理的应用，解决本题的关键是作出辅助线．