
 如图,已知二次函数y=-x2-3x+4的图象与x轴的交于A,B两点,与y轴交于点C.一次函数的图象过点A、C.
如图,已知二次函数y=-x2-3x+4的图象与x轴的交于A,B两点,与y轴交于点C.一次函数的图象过点A、C.分析 (1)由抛物线解析式可分别求出点A、点C、点B的坐标,由此可得AB,OC的长,再由三角形的面积公式即可得到△ABC的面积.
(2)设过A、C的直线解析式为y=kx+b,把点A、C的坐标分别代入求出k和b的值即可.
(3)利用函数图象结合交点坐标得出使一次函数值大于二次函数值的x的取值范围.
解答 解:(1)设y=0,则0=-x2-3x+4,
解得x=-1或4,
∴点A(4,0),点B(-1,0),
∴AB=5,
设x=0,则y=4,
∴点C的坐标为(0,4),
即OC=4,
∴△ABC的面积=$\frac{1}{2}$×5×4=10;
(2)设过A、C的直线解析式为y=kx+b,
则$\left\{\begin{array}{l}{0=4k+b}\\{4=b}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-1}\\{b=4}\end{array}\right.$,
所以一次函数的解析式是y=-x+4;
(3)如图,一次函数值大于二次函数值的x的取值范围是:x<0或x>4.
故答案为:x<0或x>4.
点评 此题主要考查了二次函数的性质,以及待定系数法求一次函数解析式和利用自变量的取值范围确定函数值大小关系,题目难度不大,非常典型.


科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,点A的纵坐标为2,点B在x轴的负半轴上,AB=AO,∠ABO=30°,直线MN经过原点O,点A关于直线MN的对称点A1在x轴的正半轴上.
如图,在平面直角坐标系中,点A的纵坐标为2,点B在x轴的负半轴上,AB=AO,∠ABO=30°,直线MN经过原点O,点A关于直线MN的对称点A1在x轴的正半轴上.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,Rt△ABC中,∠C=90°,AC=3,BC=4,点D在AB边上,点E是BC边上一点(不与点B、C重合),且DA=DE,则AD的取值范围是( )
如图,Rt△ABC中,∠C=90°,AC=3,BC=4,点D在AB边上,点E是BC边上一点(不与点B、C重合),且DA=DE,则AD的取值范围是( )| A. | 0<AD<3 | B. | 1≤AD<$\frac{5}{2}$ | C. | $\frac{15}{7}$≤AD<$\frac{5}{2}$ | D. | $\frac{15}{8}$≤AD<$\frac{5}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,⊙Q交坐标轴于A,B,C,D,点P在弦EB的延长线上,且BC平分∠ABP.
如图,在平面直角坐标系中,⊙Q交坐标轴于A,B,C,D,点P在弦EB的延长线上,且BC平分∠ABP.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,O为直线AB上一点,OD平分∠AOC,OE平分∠COB,
如图,O为直线AB上一点,OD平分∠AOC,OE平分∠COB,查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
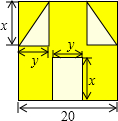 “囧”像一个人脸郁闷的神情.如图,边长为a的正方形纸片,剪去两个一样的小直角三角形和一个长方形得到一个“囧”字图案(阴影部分),设剪去的两个小直角三角形的两直角边长分别为x、y,剪去的小长方形长和宽也分别为x,y.
“囧”像一个人脸郁闷的神情.如图,边长为a的正方形纸片,剪去两个一样的小直角三角形和一个长方形得到一个“囧”字图案(阴影部分),设剪去的两个小直角三角形的两直角边长分别为x、y,剪去的小长方形长和宽也分别为x,y.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,现实生活中有部分行人选择横穿马路而不走天桥或斑马线,用数学知识解释这一现象的原因,可以为( )
如图,现实生活中有部分行人选择横穿马路而不走天桥或斑马线,用数学知识解释这一现象的原因,可以为( )| A. | 过一点有无数条直线 | |
| B. | 两点之间线段的长度,叫做这两点之间的距离 | |
| C. | 两点确定一条直线 | |
| D. | 两点之间,线段最短 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com