Question

10．如图，正方形ABCD的边长为6cm，E为CD边上一点，∠DAE=30°，M为AE的中点，过点M作直线分别与AD、BC相交于点P、Q．若PQ=AE，则AP等于2或4cm．

Answer 1

分析 先由三角函数求出AE，得出AM，再证明Rt△PFQ≌Rt△ADE，得出∠FPQ=∠DAE，然后分两种情况分别作图求出AP即可．

解答 解：∵∠DAE=30°，
∴AE=$\frac{AD}{cos30°}$=$\frac{6}{\frac{\sqrt{3}}{2}}$4$\sqrt{3}$（cm），
∵M为AE的中点，
∴AM=2$\sqrt{3}$cm，
①如图1作PF⊥BC于F，交AE与G，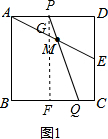
则∠PFQ=90°，PF=AD，
在Rt△PFQ和Rt△ADE中，
$\left\{\begin{array}{l}{PQ=AE}\\{PF=AD}\end{array}\right.$，
∴Rt△PFQ≌Rt△ADE（HL），
∴∠FPQ=∠DAE=30°，
∴∠APM=90°+30°=120°，
∴∠AMP=30°，
∴∠DAE=∠AMP=30°，
∵∠AMP=∠PMG，
∴△APM∽△PGM，
∴$\frac{AP}{PG}$=$\frac{AM}{AP}$，
∴cot30°=$\frac{AP}{PG}$=$\sqrt{3}$，
∴$\frac{AM}{AP}$=$\sqrt{3}$，
即$\frac{2\sqrt{3}}{AP}$=$\sqrt{3}$
∴AP=2cm．
②如图2所示：作PF⊥BC于F，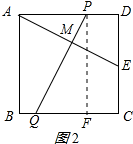
同理Rt△PFQ≌Rt△ADE，
∴∠FPQ=∠DAE，
∵∠FPQ+∠APM=90°，
∴∠DAE+∠APM=90°，
∴∠AMP=90°=∠D，
∵∠PAM=∠DAE，
∴△APM∽△AED，
∴$\frac{AP}{AE}$=$\frac{AM}{AD}$，
即$\frac{AP}{4\sqrt{3}}$=$\frac{2\sqrt{3}}{6}$，
∴AP=4cm．
故答案为2或4．

点评 本题考查了正方形的性质、全等三角形的判定与性质、三角函数、相似三角形的判定与性质；熟练掌握正方形的性质，并能进行推理论证与计算是解决问题的关键．