
分析 (1)按照运算规则,逐个找出数列的前六项;
(2)按照运算规则,逐个找出数列的前六项;
(3)结合(1)(2)发现该规则下的数列以3为周期,按照a1、a2、a3循环的,再结合2015÷3=671…2,即可得出结论.
解答 解:数列中第n项用an来代替.
(1)按照规则:a1=3,a2=1-$\frac{1}{{a}_{1}}$=$\frac{2}{3}$,a3=1-$\frac{1}{{a}_{2}}$=-$\frac{1}{2}$,a4=1-$\frac{1}{{a}_{3}}$=3,a5=1-$\frac{1}{{a}_{4}}$=$\frac{2}{3}$,a6=1-$\frac{1}{{a}_{5}}$=-$\frac{1}{2}$.
故首项是3的数列的前6项为:3,$\frac{2}{3}$,-$\frac{1}{2}$,3,$\frac{2}{3}$,-$\frac{1}{2}$.
(2)按照规则:a1=x,a2=1-$\frac{1}{{a}_{1}}$=$\frac{x-1}{x}$,a3=1-$\frac{1}{{a}_{2}}$=-$\frac{1}{x-1}$,a4=1-$\frac{1}{{a}_{3}}$=x,a5=1-$\frac{1}{{a}_{4}}$=$\frac{x-1}{x}$,a6=1-$\frac{1}{{a}_{5}}$=-$\frac{1}{x-1}$.
故首项是x的数列的前6项为:x,$\frac{x-1}{x}$,-$\frac{1}{x-1}$,x,$\frac{x-1}{x}$,-$\frac{1}{x-1}$.
(3)结合(1)(2)发现数列是以3为周期,按照前三个数一直循环的.
∵2015÷3=671…2,而a1×a2×a3=x•$\frac{x-1}{x}$•$\frac{-1}{x-1}$=-1,
∴a1×a2×a3×…×a2015=(-1)671×a1×a2=1-x.
故首项是x的数列的前2015项的乘积为1-x.
点评 本题考查了数字的变化,解题的关键是:(1)(2)按照运算规则,逐项列出前六项;(3)发现该规则下的数列以3为周期,按照a1、a2、a3循环的.本题属于中档题型,(1)(2)难度不大,(3)稍微有点难度,需要在前面结果的基础上找到循环的规律.


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:初中数学 来源: 题型:选择题
| A. | a=b | B. | $|a|=\sqrt{b^2}$ | C. | a3=b3 | D. | $\sqrt{a}=\sqrt{b}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
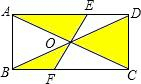 如图,矩形ABCD中,对角线AC、BD交于点O,过O的直线分别交AD、BC于点E、F,已知AD=4cm,图中阴影部分的面积总和为6cm2,对角线AC长为( )
如图,矩形ABCD中,对角线AC、BD交于点O,过O的直线分别交AD、BC于点E、F,已知AD=4cm,图中阴影部分的面积总和为6cm2,对角线AC长为( )| A. | 3cm | B. | 4cm | C. | 5cm | D. | 6cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,方格纸中每个小正方形的边长都是1个单位长度.Rt△ABC的三个顶点A(-2,2),B(0,5),C(0,2)
如图,方格纸中每个小正方形的边长都是1个单位长度.Rt△ABC的三个顶点A(-2,2),B(0,5),C(0,2)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com