
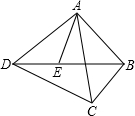
 如图,点E是四边形ABCD的对角线BD上一点,且∠BAC=∠BDC=∠DAE.
如图,点E是四边形ABCD的对角线BD上一点,且∠BAC=∠BDC=∠DAE.| BC |
| DE |
| BC |
| DE |
| AB |
| AE |
| AC |
| AD |
| BC |
| DE |
| AB |
| AE |
| AC |
| AD |
| AB |
| AC |
| AE |
| AD |
| BC |
| DE |
| AB |
| AE |
| AC |
| AD |
| BC |
| DE |
| AB |
| AE |
| AC |
| AD |


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
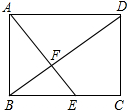 如图,四边形ABCD是矩形,点E在BC边上,AE与BD交于点F,∠BAE=∠ADB.
如图,四边形ABCD是矩形,点E在BC边上,AE与BD交于点F,∠BAE=∠ADB.查看答案和解析>>
科目:初中数学 来源: 题型:
| A、抛一枚硬币,落地后国徽一面朝下 |
| B、随意翻一下日历,翻到的号数是偶数 |
| C、这个月有雨 |
| D、今年夏天的最高气温达到了100℃ |
查看答案和解析>>
科目:初中数学 来源: 题型:
|
|
型号 | A型包装 | B型包装 | C型包装 |
| 每盒装 | 毛尖1千克 | 龙井1千克 | 毛尖0.4千克;龙井0.6千克 |
| 每盒价格 | 45元 | 60元 | 56元 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 已知,在如图的数轴上有A、B、C三点,它们所表示的数依次是-1,+5和x.
已知,在如图的数轴上有A、B、C三点,它们所表示的数依次是-1,+5和x.| 10 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com