
【题目】如图,△ABC是⊙O的内接三角形,直径AB垂直于弦CG,垂足为点H,过点C作ED⊥CG,交⊙O于点E,且∠CBD=∠A,连接BE,交CG于点F.
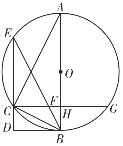
(1)求证:BD是⊙O的切线;
(2)求证:BC2=BF·BE;
(3)若CG=8,AB=10,求sin E的值.
【答案】(1)见解析;(2)见解析;(3)sin E=![]() .
.
【解析】
(1)利用直径所对的圆周角是直角,易证得∠ABD=90°,从而证得结论;
(2)利用垂径定理结合圆周角定理证得∠BCG=∠E,得到△CBF∽△EBC,利用对应边成比例,即可证明结论;
(3)连接OC,利用垂径定理求得CH =4,在Rt△OCH中,由勾股定理求得OH的长,在Rt△BCH中,由勾股定理求得BC的长,由于∠E=∠BCG,利用正弦函数即可求解.
(1)证明:∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠A+∠CBA=90°.
∵∠CBD=∠A,
∴∠CBA+∠CBD=90°,即∠ABD=90°,
∴AB⊥BD,
∵OB是⊙O的半径,
∴BD是⊙O的切线;
(2)证明:∵AB⊥CG,
∴![]() =
=![]() ,
,
∴∠BCG=∠E,
又∠CBF=∠EBC,
∴△CBF∽△EBC,
∴![]() ,
,
∴BC2=BF·BE;
(3)连接OC.
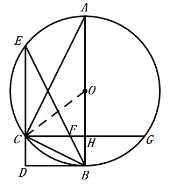
∵AB=10,CG=8,AB⊥CG,
∴CH=![]() CG=4,OB=OC=
CG=4,OB=OC=![]() AB=5,
AB=5,
在Rt△OCH中,由勾股定理,得OH=![]() ,
,
∴BH=OB-OH=2,
在Rt△BCH中,由勾股定理,得BC=![]() ,
,
由(2)得∠E=∠BCG,
∴sin E=sin∠BCG=![]() .
.


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案科目:初中数学 来源: 题型:
【题目】如图,已知A(n,![]() 2),B(
2),B(![]() 1,4)是一次函数y=kx+b和反比例函数y=
1,4)是一次函数y=kx+b和反比例函数y=![]() 的图象的两个交点.
的图象的两个交点.
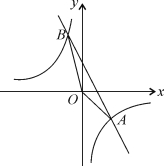
(1)求反比例函数和一次函数的解析式;
(2)求△AOB的面积.
(3)直接写出kx+b>![]() 时,
时,![]() 的取值范围为 .
的取值范围为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某人开车从家出发去植物园游玩,设汽车行驶的路程为S(千米),所用时间为t(分),S与t之间的函数关系如图所示.若他早上8点从家出发,汽车在途中停车加油一次,则下列描述中,不正确的是( )
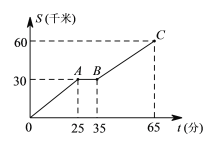
A.汽车行驶到一半路程时,停车加油用时10分钟
B.汽车一共行驶了60千米的路程,上午9点5分到达植物园
C.加油后汽车行驶的速度为60千米/时
D.加油后汽车行驶的速度比加油前汽车行驶的速度快
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某医院医生为了研究该院某种疾病的诊断情况,需要调查来院就诊的病人的两个生理指标![]() ,
,![]() ,于是他分别在这种疾病的患者和非患者中,各随机选取20人作为调查对象,将收集到的数据整理后,绘制统计图如下:
,于是他分别在这种疾病的患者和非患者中,各随机选取20人作为调查对象,将收集到的数据整理后,绘制统计图如下:
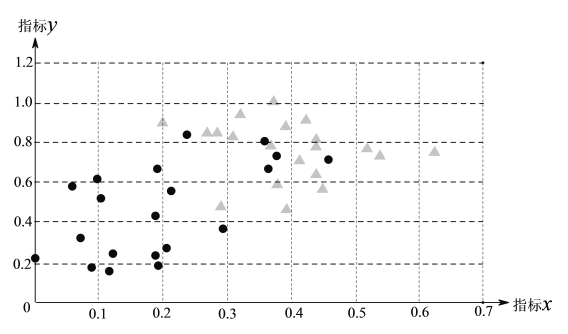
注“●”表示患者,“▲”表示非患者.
根据以上信息,回答下列问题:
(1)在这40名被调查者中,
①指标![]() 低于0.4的有 人;
低于0.4的有 人;
②将20名患者的指标![]() 的平均数记作
的平均数记作![]() ,方差记作
,方差记作![]() ,20名非患者的指标
,20名非患者的指标![]() 的平均数记作
的平均数记作![]() ,方差记作
,方差记作![]() ,则
,则![]()
![]() ,
,![]()
![]() (填“>”,“=”或“<”);
(填“>”,“=”或“<”);
(2)来该院就诊的500名未患这种疾病的人中,估计指标![]() 低于0.3的大约有 人;
低于0.3的大约有 人;
(3)若将“指标![]() 低于0.3,且指标
低于0.3,且指标![]() 低于0.8”作为判断是否患有这种疾病的依据,则发生漏判的概率多少.
低于0.8”作为判断是否患有这种疾病的依据,则发生漏判的概率多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,AB=2,AD=4,对角线AC,BD相交于点O,且E,F,G,H分别是AO,BO,CO,DO的中点,则下列说法正确的是( )
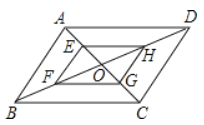
A.EH=HGB.四边形EFGH是平行四边形
C.AC⊥BDD.![]() 的面积是
的面积是![]() 的面积的2倍
的面积的2倍
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校初三(1)班部分同学接受一次内容为“最适合自己的考前减压方式”的调查活动,收集整理数据后,老师将减压方式分为五类,并绘制了图1、图2两个不完整的统计图,请根据图中的信息解答下列问题.
(1)初三(1)班接受调查的同学共有多少名;
(2)补全条形统计图,并计算扇形统计图中的“体育活动C”所对应的圆心角度数;
(3)若喜欢“交流谈心”的5名同学中有三名男生和两名女生;老师想从5名同学中任选两名同学进行交流,直接写出选取的两名同学都是女生的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某教研机构为了了解初中生课外阅读名著的现状,随机抽取了某校50名初中生进行调查,依据相关数据绘制成了以下不完整的统计图,请根据图中信息解答下列问题:
类别 | 重视 | 一般 | 不重视 |
人数 | a | 15 | b |
(1)求表格中a,b的值;
(2)请补全统计图;
(3)若某校共有初中生2000名,请估计该校“重视课外阅读名著”的初中生人数.
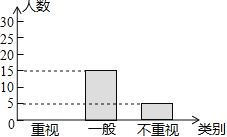
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面内的点![]() 与射线
与射线![]() ,射线
,射线![]() 上与点
上与点![]() 距离最近的点与端点
距离最近的点与端点![]() 的距离叫做点
的距离叫做点![]() 关于射线
关于射线![]() 的侧边距,记作
的侧边距,记作![]() .
.

(1)在菱形![]() 中,
中,![]() ,
,![]() .则
.则![]() __________,
__________,![]() __________.
__________.
(2)在![]() 中,若
中,若![]() ,则
,则![]() 是否必为正方形,请说明理由;
是否必为正方形,请说明理由;
(3)如图,已知点![]() 是射线
是射线![]() 上一点,
上一点,![]() ,以
,以![]() 为半径画
为半径画![]() ,点
,点![]() 是
是![]() 上任意点,
上任意点,![]() 为线段
为线段![]() 的中点.
的中点.
①若![]() ,则
,则![]() __________;
__________;
②设![]() ,
,![]() ,求
,求![]() 关于
关于![]() 的函数关系式并写出自变量
的函数关系式并写出自变量![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为培养学生庭好的学习习惯,某校九年级年级组举行“整理错题集“的征集展示活动,并随机对部分学生三年“整理题集”中收集的错题数x进行了抽样调查,根据收集的数据绘制了下面不完整的统计图表.
分组 | 频数 | 频率 |
第一组(0≤x<120) | 3 | 0.15 |
第二组(120≤x<160) | 8 | a |
第三组(160≤x<200) | 7 | 0.35 |
第四组(200≤x<240) | b | 0.1 |
请你根据图表中的信息完成下列问题:
(1)频数分布表中a= ,b= ,并将统计图补充完整;
(2)如果该校九年级共有学生360人,估计整理的错题数在160或160题以上的学生有多少人?
(3)已知第一组中有两个是甲班学生,第四组中有一个是甲班学生,老师随机从这两个组中各选一名学生谈整理错题的体会,则所选两人正好都是甲班学生的概率是多少?
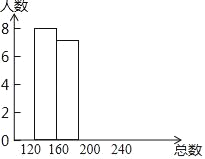
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com