
【题目】△ABC中,AC=BC,∠ACB=90°,点D在AB上,点E在BC上,且AD=BE,BD=AC,连DE、CD.
(1)找出图中全等图形,并证明;
(2)求∠ACD的度数;

【答案】(1)△ADC≌△BED,证明见解析;(2)∠ACD=22.5°.
【解析】
(1)由“SAS”可证△ADC≌△BED;
(2)由全等三角形的性质可得∠ACD=∠BDE,CD=DE,由外角性质和等腰三角形的性质可求∠DCE=67.5°,即可求解.
(1)△ADC≌△BED,
理由如下:∵AC=BC,∠ACB=90°,
∴∠A=∠B=45°,且AD=BE,BD=AC,
∴△ADC≌△BED(SAS)
(2)∵△ADC≌△BED,
∴∠ACD=∠BDE,CD=DE,
∵∠BDC=∠A+∠ACD=∠CDE+∠BDE,
∴∠CDE=∠A=45°,且DC=DE,
∴∠DCE=67.5°,
∴∠ACD=∠ACB﹣∠DCE=22.5°.


 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点B的坐标是(0,2),动点A从原点O出发,沿着x轴正方向移动,△ABP是以AB为斜边的等腰直角三角形(点A、B、P顺时针方向排列),当点A与原点O重合时,得到等腰直角△OBC(此时点P与点C重合).
(1)BC=______;当OA=2时,点P的坐标是______;
(2)设动点A的坐标为(t,0)(t≥0).
①求证:点A在移动过程中,△ABP的顶点P一定在射线OC上;
②用含t的代数式表示点P的坐标为:(______,______);
(3)过点P做y轴的垂线PQ,Q为垂足,当t=______时,△PQB与△PCB全等.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】人民商场销售某种商品,统计发现:每件盈利![]() 元时,平均每天可销售
元时,平均每天可销售![]() 件.经调查发现,该商品每降价
件.经调查发现,该商品每降价![]() 元,商场平均每天可多售出
元,商场平均每天可多售出![]() 件.
件.
![]() 假如现在库存量太大,部门经理想尽快减少库存,又想销售该商品日盈利达到
假如现在库存量太大,部门经理想尽快减少库存,又想销售该商品日盈利达到![]() 元,请你帮忙思考,该降价多少?
元,请你帮忙思考,该降价多少?
![]() 假如部门经理想销售该商品的日盈利达到最大,请你帮忙思考,又该如何降价?
假如部门经理想销售该商品的日盈利达到最大,请你帮忙思考,又该如何降价?
查看答案和解析>>
科目:初中数学 来源: 题型:
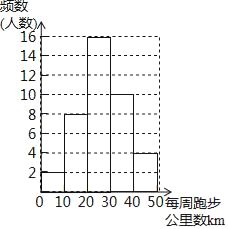
【题目】某市举行主题为“奔跑吧!2018”的市民健康跑活动.红树林学校的小记者随机采访了40名参赛选手,了解到他们平时每周跑步公里数(单位:km),并根据统计结果绘制出以下频数分布直方图和不完整的表格.
每周跑步公里数/km | 频数(人数) | 频率 |
0≤x<10 | 2 | 5% |
10≤x<20 | a | m |
20≤x<30 | b | 40% |
30≤x<40 | 10 | 25% |
40≤x<50 | 4 | n |
(1)求a= ,n= ;
(2)本次活动有10000人参加比赛,请根据上述调查结果,估算该活动中每周跑步公里数在10≤x<30 内的人数;
(3)应比赛组委会要求,现从每周跑步公里数在40≤x<50 内的4名参赛选手甲,乙,丙,丁中随机抽取2人作为本次活动的形象宣传员,请用画树状图法或列表法求出恰好抽中乙,丙两人的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
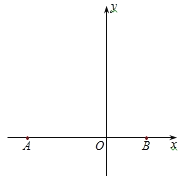
【题目】如图所示,已知等边△ABC的两个顶点的坐标为A(-4,0),B(2,0).
(1)用尺规作图作出点C,并求出点C的坐标;
(2)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在任意四边形ABCD中,AC,BD是对角线,E、F、G、H分别是线段BD、BC、AC、AD上的点,对于四边形EFGH的形状,某班的学生在一次数学活动课中,通过动手实践,探索出如下结论,其中错误的是( )

A. 当E,F,G,H是各条线段的中点时,四边形EFGH为平行四边形
B. 当E,F,G,H是各条线段的中点,且AC⊥BD时,四边形EFGH为矩形
C. 当E,F,G,H是各条线段的中点,且AB=CD时,四边形EFGH为菱形
D. 当E,F,G,H不是各条线段的中点时,四边形EFGH可以为平行四边形
查看答案和解析>>
科目:初中数学 来源: 题型:
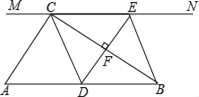
【题目】如图:在Rt△ABC中,∠ACB=90°,AB=6,过点C的直线MN∥AB,D为AB上一点,过点D作DE⊥BC,交直线MN于点E,垂足为F,连结CD,BE,
(1)当点D是AB的中点时,四边形BECD是什么特殊四边形?说明你的理由
(2)在(1)的条件下,当∠A= 时四边形BECD是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD平分∠BAC,点P为线段AD上的一个动点,PE⊥AD交BC的延长线于点E.
(1)若∠B=35°,∠ACB=85°,求∠E得度数.
(2)当点P在线段AD上运动时,设∠B=α,∠ACB=β(β>α),求∠E得大小.(用含α、β的代数式表示)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com