
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 是射线
是射线![]() 上一动点,连接
上一动点,连接![]() ,将
,将![]() 沿
沿![]() 折叠,当点
折叠,当点![]() 的对应点
的对应点![]() 落在线段
落在线段![]() 的垂直平分线上时,
的垂直平分线上时,![]() 的长等于__________.
的长等于__________.

【答案】![]() 或10.
或10.
【解析】
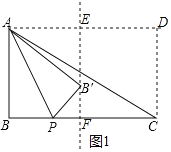
①如图1,当点P在线段BC上时,②如图2,当点P在BC的延长线上时,过A,C分别作AD∥BC,CD∥AB两线交于D,得到四边形ABCD是矩形,求得AD=BC=8,过B′作B′F⊥BC于F,反向延长FB′交AD于E,根据勾股定理即可得到结论.
解:①如图1,当点P在线段BC上时,
过A,C分别作AD∥BC,CD∥AB两线交于D, 则四边形ABCD是矩形,
∴AD=BC=8, 过B′作B′F⊥BC于F,反向延长FB′交AD于E, 则AD⊥EF,
∵点B'落在线段BC的垂直平分线上,
∴AE=BF=![]() BC=4,
BC=4,
∵将△ABP沿AP折叠得到△AB′P,
∴AB′=AB=5,PB=PB′,
∴EB′=3, ∴B′F=2,
∴PF=4-PB,
∵![]() ,
,
∴![]() ,
,
解得:![]()
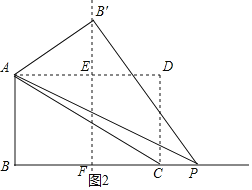
②如图2,当点P在BC的延长线上时, 过A,C分别作AD∥BC,CD∥AB两线交于D, 则四边形ABCD是矩形,
∴AD=BC=8, 过B′作B′F⊥BC于F,反向延长FB′交AD于E, 则AD⊥EF,
∵点B'落在线段BC的垂直平分线上,
∴AE=BF=![]() BC=4,
BC=4,
∵将△ABP沿AP折叠得到△AB′P,
∴AB′=AB=5,PB=PB′,
∴EB′=3, ∴B′F=8,
∴PF=PB-4,
∵![]() ,
,
∴![]()
解得:BP=10;
综上所述,BP的长等于![]() 或10,
或10,
故答案为: ![]() 或10.
或10.


科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2-mx+n图像的顶点为C(1,-4).
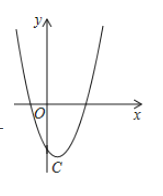
(1)求二次函数的表达式;
(2)如点A是二次函数在第四象限内图象上的一动点,过点A作![]() 轴,P为垂足,求
轴,P为垂足,求![]() 的最大值;
的最大值;
(3)已知点B(-1,-4),问在的对称轴上是否存在点Q,使线段QB绕点Q顺时针旋转![]() 得到线段
得到线段![]() ,且点
,且点![]() 恰好落在二次函数图像上?若存在,求出点Q的坐标;若不存在,请说明理由.
恰好落在二次函数图像上?若存在,求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】武汉某超市在疫情前用3000元购进某种干果销售,发生疫情后,为了保障附近居民的生活需求,又调拨9000元购进该种干果.受疫情影响,交通等成本上涨,第二次的进价比第一次进价提高了20%,但是第二次购进干果的数量是第一次的2倍还多300千克,如果超市先按每千克9元的价格出售,当大部分干果售出后,最后的600千克按原售价的7折售完.售卖结束后,超市决定将盈利的资金捐助给武汉市用于抗击新冠肺炎疫情.那么该超市可以捐助___________元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1.有下列结论:①b2=4ac ②abc>0 ③a>c ④4a+c>2b.其中结论正确的个数是( )
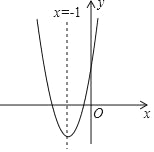
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程kx2﹣2(k+1)x+k﹣1=0有两个不相等的实数根x1,x2.
(1)求k的取值范围;
(2)是否存在实数k,使![]() =1成立?若存在,请求出k的值;若不存在,请说明理由.
=1成立?若存在,请求出k的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在全国预防“新冠肺炎”时期,某厂接受了生产一批高质量医用口罩的任务.要求8天之内(含8天)生产![]() 型和
型和![]() 型两种型号的口罩共5万只,其中
型两种型号的口罩共5万只,其中![]() 型口罩不得少于1.8万只.该厂的生产能力是:每天只能生产一种型号的口罩,若生产
型口罩不得少于1.8万只.该厂的生产能力是:每天只能生产一种型号的口罩,若生产![]() 型口罩每天能生产0.6万只,若生产
型口罩每天能生产0.6万只,若生产![]() 型口罩每天能生产0.8万只.已知生产6只
型口罩每天能生产0.8万只.已知生产6只![]() 型和10只
型和10只![]() 型口罩一共获利6元,生产4只
型口罩一共获利6元,生产4只![]() 型和5只
型和5只![]() 型口罩一共获利3.5元
型口罩一共获利3.5元
(1)生产一只![]() 型口罩和
型口罩和![]() 型口罩分别获利多少钱?
型口罩分别获利多少钱?
(2)若生产![]() 型口罩
型口罩![]() 万只,该厂这次生产口罩的总利润为
万只,该厂这次生产口罩的总利润为![]() 万元,请求出
万元,请求出![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(3)在完成任务的前提下,如何安排生产![]() 型和
型和![]() 型口罩的只数,使获得的总利润最大?最大利润是多少?
型口罩的只数,使获得的总利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】工厂甲、乙两个部门各有员工400人,为了解这两个部门员工的生产技能情况,进行了抽样调查,请将下列过程补充完整:
收集数据:
从甲、乙两个部门各随机抽取20名员工,进行了生产技能测试,测试成绩(百分制)如下:

整理、描述数据:
按如下分数段整理、描述这两组样本数据:
成绩 人数 部门 | 40≤x≤49 | 50≤x≤59 | 60≤x≤69 | 70≤x≤79 | 80≤x≤89 | 90≤x≤100 |
甲 | 0 | 0 | 1 | 11 | 7 | 1 |
乙 |
(说明:成绩80分及以上为生产技能优秀,70—79分为生产技能良好,60—69分为生产技能合格,60分以下为生产技能不合格)
分析数据:
两组样本数据的平均数、中位数、众数如下表所示:
部门 | 平均数 | 中位数 | 众数 |
甲 | 78.3 | 77.5 | |
乙 | 78 | 81 |
得出结论:
![]() .估计乙部门生产技能优秀的员工人数约为 .
.估计乙部门生产技能优秀的员工人数约为 .
![]() .可以推断出 部门员工的生产技能水平高.理由为 .
.可以推断出 部门员工的生产技能水平高.理由为 .
(至少从两个不同的角度说明推断的合理性)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上,李老师准备了四张背面都一样的卡片A、B、C、D,每张卡片的正面标有字母a、b、c表示三条线段(如下图).把四张卡片背面朝上放在桌面上,李老师从这四张卡片中随机抽取一张卡片后不放回,再随机抽取一张.

⑴ 李老师随机抽取一张卡片,抽到卡片B的概率等于 ;
⑵ 求李老师抽取的两张卡片中每张卡片上的三条线段都能组成三角形的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
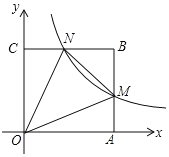
【题目】如图,在平面直角坐标系中,边长为1的正方形OABC的顶点O与原点重合,顶点A,C分别在x轴、y轴上,反比例函数y=![]() (k≠0,x>0)的图象与正方形的两边AB、BC分别交于点M、N,连接OM、ON、MN.若∠MON=45°,则k的值为_____.
(k≠0,x>0)的图象与正方形的两边AB、BC分别交于点M、N,连接OM、ON、MN.若∠MON=45°,则k的值为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com