
【题目】已知二次函数y=x2-mx+n图像的顶点为C(1,-4).
(1)求二次函数的表达式;
(2)如点A是二次函数在第四象限内图象上的一动点,过点A作![]() 轴,P为垂足,求
轴,P为垂足,求![]() 的最大值;
的最大值;
(3)已知点B(-1,-4),问在的对称轴上是否存在点Q,使线段QB绕点Q顺时针旋转![]() 得到线段
得到线段![]() ,且点
,且点![]() 恰好落在二次函数图像上?若存在,求出点Q的坐标;若不存在,请说明理由.
恰好落在二次函数图像上?若存在,求出点Q的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)存在,Q(1,﹣5)或Q(1,﹣2)
;(3)存在,Q(1,﹣5)或Q(1,﹣2)
【解析】
(1)二次函数y=x2-mx+n图像的顶点为C(1,-4),即可求m,n;
(2)作AP⊥x轴,设A(a,a2-2a-3),所以AP=-a2+2a+3,PO=a,可得AP+OP=-a2+3a+3=![]() ,由已知可知0<a<3,即可求;
,由已知可知0<a<3,即可求;
(3)假设对称轴上存在点Q,过点B'作B'D⊥对称轴l于点D,可得∠B'DQ=90°;①当点Q在顶点C的下方时,可证△BCQ≌△QDB',设点Q(1,b),所以B'D=CQ=-4-b,QD=BC=2,可知B'(-3-b,2+b),可得![]() ,可求b=-5,Q(1,-5),②当点Q在顶点C的上方时,同理可得Q(1,-2).
,可求b=-5,Q(1,-5),②当点Q在顶点C的上方时,同理可得Q(1,-2).
(1)∵二次函数y=x2-mx+n图像的顶点为C(1,-4),
∴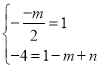
∴![]()
∴![]()
(2)作AP⊥x轴,设A(a,![]() )
)
∵A在第四象限,
∴0<a<3,
∴![]()
∴![]()
∵0<a<3,![]()
∴当![]() 时AP+OP的最大值为
时AP+OP的最大值为![]()
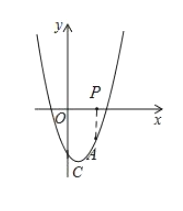
(3)假设对称轴上存在点Q,过点![]() 作
作![]() 于点D
于点D

∴![]()
①当点Q在顶点C的下方时
∵B(﹣1,﹣4),C(1,﹣4),抛物线的对称轴为x=1
∴BC⊥l,BC=2,∠BCQ=90°
∴△BCQ≌△QDB'
∴B'D=CQ,QD=BC,
设点Q(1,b)
∴B'D=CQ=-4-b,QD=BC=2,
可知B'(-3-b,2+b),
∴![]()
∴![]()
∴b=-2或b=-5,
∵b<-4,
∴Q(1,﹣5),
②当点Q在顶点C的上方时,同理可得Q(1,﹣2);
综上所述:Q(1,﹣5)或Q(1,﹣2);


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图1,圆内接四边形ABCD,AD=BC,AB是⊙O的直径.
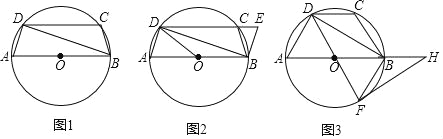
(1)求证:AB∥CD;
(2)如图2,连接OD,作∠CBE=2∠ABD,BE交DC的延长线于点E,若AB=6,AD=2,求CE的长;
(3)如图3,延长OB使得BH=OB,DF是⊙O的直径,连接FH,若BD=FH,求证:FH是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
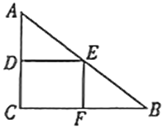
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,矩形
,矩形![]() 的顶点
的顶点![]() 在边
在边![]() 上,
上,![]() ,
,![]() 两点分别在边
两点分别在边![]() ,
,![]() 上,且
上,且![]() .将矩形
.将矩形![]() 以每秒1个单位长度的速度沿射线
以每秒1个单位长度的速度沿射线![]() 方向匀速运动,当点
方向匀速运动,当点![]() 与点
与点![]() 重合时停止运动,设运动时间为
重合时停止运动,设运动时间为![]() 秒,矩形
秒,矩形![]() 与
与![]() 重叠部分的面积为
重叠部分的面积为![]() ,则反映
,则反映![]() 与
与![]() 的函数关系的图象为( )
的函数关系的图象为( )
A.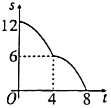 B.
B.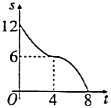 C.
C.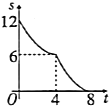 D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:在教学课上,老师提出如下问题:尺规作图:作一条线段的垂直平分线.
已知:线段AB.
![]()
求作:线段AB的垂直平分线.
小芸的作法如下:如图, (1)分别以点A和点B为圆心,大于![]() 的长为半径作弧,两孤相交于C,D两点; (2)作直线CD.所以直线CD就是所求作的垂直平分线.
的长为半径作弧,两孤相交于C,D两点; (2)作直线CD.所以直线CD就是所求作的垂直平分线.
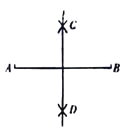
老师说:“小芸的作法正确.”
请回答:小芸的作图依据是____________________,
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2020年初,新冠肺炎肆虐全球.我国政府和人民采取了积极有效的防疫措施,疫情在我国得到了有效控制.小明为复学到药店购买![]() 口罩和一次性医用口罩.已知购买
口罩和一次性医用口罩.已知购买![]() 个
个![]() 口罩和
口罩和![]() 个一次性医用口罩共需
个一次性医用口罩共需![]() 元;购买
元;购买![]() 个
个![]() 口罩和
口罩和![]() 个一次性医用罩共需
个一次性医用罩共需![]() 元.
元.
(1)求![]() 口罩与一次性医用口罩的单价;
口罩与一次性医用口罩的单价;
(2)小明准备购买![]() 口罩和一次性医用口罩共
口罩和一次性医用口罩共![]() 个,且
个,且![]() 口罩的数量不少于一次性医用口罩数量的
口罩的数量不少于一次性医用口罩数量的![]() .请设计出最省钱的购买方案,并说明理由.
.请设计出最省钱的购买方案,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
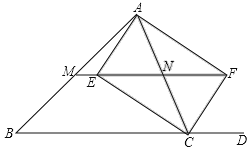
【题目】如图:在△ABC中,CE、CF分别平分∠ACB与它的邻补角∠ACD,AE⊥CE于E,AF⊥CF于F,直线EF分别交AB、AC于M、N.
(1)求证:四边形AECF为矩形;
(2)试猜想MN与BC的关系,并证明你的猜想;
(3)如果四边形AECF是菱形,试判断△ABC的形状,直接写出结果,不用说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点P(﹣1,m)是双曲线y=![]() 上的一个点,过点P作PQ⊥x轴于点Q,连接PO,△OPQ的面积为3.
上的一个点,过点P作PQ⊥x轴于点Q,连接PO,△OPQ的面积为3.

(1)求m的值和双曲线对应的函数表达式;
(2)若经过点P的一次函数y=kx+b(k≠0、b≠0)的图象与x轴交于点A,与y交于点B且PB=2AB,求k的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com