

|
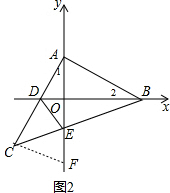 证明:作CF⊥AC交y轴于F,如图2,
证明:作CF⊥AC交y轴于F,如图2,
|
|


 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案科目:初中数学 来源: 题型:
| 乘车次数n | 余额y(元) |
| 1 | 50-1.8=48.2 |
| 2 | 50-3.6=36.4 |
| 3 | 50-5.4=34.6 |
| … | … |
查看答案和解析>>
科目:初中数学 来源: 题型:
| A、1.4960×108km |
| B、1.4960×107km |
| C、1.4960×1010km |
| D、1.4960×1011km |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在Rt△ABC中,AB=AC,D,E是斜边BC上两点,且∠DAE=45°,将△ADC绕点A顺时针旋转90°后,得到△AFB,连接EF,下列结论:①△AED≌△AEF,②△ABE≌△ACD;③BE+DC=DE;④BE2+DC2=DE2,其中正确的是
如图,在Rt△ABC中,AB=AC,D,E是斜边BC上两点,且∠DAE=45°,将△ADC绕点A顺时针旋转90°后,得到△AFB,连接EF,下列结论:①△AED≌△AEF,②△ABE≌△ACD;③BE+DC=DE;④BE2+DC2=DE2,其中正确的是查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在△ABC中,P为BC上的一点,PR⊥AB,垂足为R,PS⊥AC,垂足为S,连接AP,AQ=PQ,PR=PS,给出下面三个结论:①∠BAP=∠CAP;②QP∥AP;③△BRP≌△CSP,其中正确结论的序号是
如图,在△ABC中,P为BC上的一点,PR⊥AB,垂足为R,PS⊥AC,垂足为S,连接AP,AQ=PQ,PR=PS,给出下面三个结论:①∠BAP=∠CAP;②QP∥AP;③△BRP≌△CSP,其中正确结论的序号是查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com