【题目】如图1，已知点E在正方形ABCD的边BC上，若∠AEF=90°，且EF交正方形外角的平分线CF于点F．

（1）图1中若点E是边BC的中点，我们可以构造两个三角形全等来证明AE=EF，请叙述你的一个构造方案，并指出是哪两个三角形全等（不要求证明）；

（2）如图2，若点E在线段BC上滑动（不与点B，C重合）．
①AE=EF是否总成立？请给出证明；
②在图2的AB边上是否存在一点M，使得四边形DMEF是平行四边形？若存在，请给予证明；若不存在，请说明理由．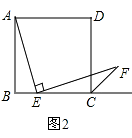

参考答案：

【答案】
（1）

解：如图1，取AB的中点G，连接EG，

△AGE与△ECF全等；


（2）

①若点E在线段BC上滑动时，AE=EF总成立．

证明：如图2，在AB上截取AH=EC，连接EH，

∵AB=BC，

∴BH=BE，

∴△HBE是等腰直角三角形，

∴∠AHE=180°﹣45°=135°，

又∵CF平分正方形的外角，

∴∠ECF=135°，

∴∠AHE=∠ECF．

而∠BAE+∠AEB=∠CEF+∠AEB=90°，

∴∠BAE=∠CEF，

∴△AHE≌△ECF，

∴AE=EF；

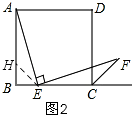
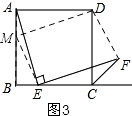
②答：存在，如图3，

过D作DM⊥AE交AB于点M，

则有：DM∥EF，连接ME、DF，

∵在△ADM与△BAE中， ，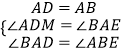

∴△ADM≌△BAE（AAS），

∴MD=AE，

∵AE=EF，

∴MD=EF，

∵MD∥EF，

∴四边形DMEP为平行四边形。


【解析】（1）作辅助线，AG=EC，∠BAE=∠CEF，∠AGE=∠ECF=180°﹣45°=135°，则△AGE≌△ECF；（2）①成立，作辅助线，仍然证明△AHE≌△ECF得出结论；②存在，如图3，过D作DM⊥AE交AB于点M，构成四边形DMEF，证明四边形为平行四边形即可．
【考点精析】本题主要考查了平行四边形的性质和平行四边形的判定的相关知识点，需要掌握平行四边形的对边相等且平行；平行四边形的对角相等，邻角互补；平行四边形的对角线互相平分；两组对边分别平行的四边形是平行四边形：两组对边分别相等的四边形是平行四边形；一组对边平行且相等的四边形是平行四边形；两组对角分别相等的四边形是平行四边形；对角线互相平分的四边形是平行四边形才能正确解答此题．

关闭