练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在平面直角坐标系中，菱形OACB的顶点O在原点，点C的坐标为（4，0），点B的纵坐标是﹣1，则顶点A坐标是（ ）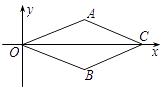

    A.（2，1）
    B.（1，﹣2）
    C.（1，2）
    D.（2，﹣1）

    【答案】A
    【解析】解：∵连接AB交OC于点D

    ∵四边形ABCD是菱形，

    ∴AB⊥OC，OD=CD，AD=BD，

    ∵点C的坐标是（4，0），点B的纵坐标是﹣1，

    ∴OC=4，BD=AD=1，

    ∴OD=CD=2，

    ∴点A的坐标为：（2，1）．

    所以答案是：A．

    【考点精析】解答此题的关键在于理解菱形的性质的相关知识，掌握菱形的四条边都相等；菱形的对角线互相垂直，并且每一条对角线平分一组对角；菱形被两条对角线分成四个全等的直角三角形；菱形的面积等于两条对角线长的积的一半．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】某校为迎接体育中考，了解学生的体育情况，学校随机调查了本校九年级50名学生“30秒跳绳”的次数，并将调查所得的数据整理如下：
    30秒跳绳次数的频数、频率分布表

    成绩段

    频数

    频率

    0≤x＜20

    5

    0.1

    20≤x＜40

    10

    a

    40≤x＜60

    b

    0.14

    60≤x＜80

    m

    c

    80≤x＜100

    12

    n

    根据以上图表信息，解答下列问题：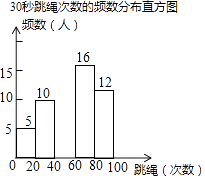

    （1）表中的a= ， m=；
    （2）请把频数分布直方图补充完整；（画图后请标注相应的数据）
    （3）若该校九年级共有600名学生，请你估计“30秒跳绳”的次数60次以上（含60次）的学生有多少人？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系中，四边形 OABC 的顶点 A、C 分别在 x 轴和 y 轴上，顶点B 在第一象限，OA//CB．

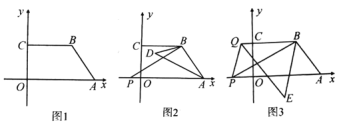
    （1）如图 1，若点 A(6，0)，B(4，3)，点 M 是 y 轴上一点，且 SBCM SAOM ，求点 M的坐标；

    （2）如图 2，点 P 是 x 轴上点 A 左边的一点，连接 PB，∠PBC 和∠PAB 的角平分线交于点D，求证：∠ABP+2∠ADB=180°；

    （3）如图 3，点 P 是 x 轴上点 A 左边的一点，点 Q 是射线 BC 上一点，连接 PB、PQ，∠ABP和∠BQP 的平分线相交于点 E，求的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，平面直角坐标系中，矩形OABC的对角线AC=12，∠ACO=30°

    （1）求B、C两点的坐标；

    （2）过点G（）作GF⊥AC，垂足为F，直线GF分别交AB、OC于点E、D，求直线DE的解析式；

    （3）在⑵的条件下，若点M在直线DE上，平面内是否存在点P，使以O、F、M、P为顶点的四边形是菱形？若存在，请直接写出点P的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

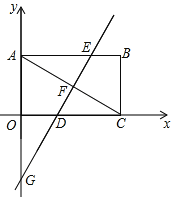
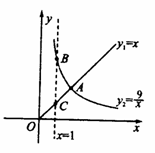
    【题目】函数 yl= x ( x ≥0 ) , （ x > 0 ）的图象如图所示，则结论： ① 两函数图象的交点A的坐标为（3 ,3 ) ② 当 x > 3 时， ③ 当 x ＝1时， BC = 8

    ④ 当 x 逐渐增大时， yl 随着 x 的增大而增大，y2随着 x 的增大而减小．其中正确结论的序号是＿ .

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某电信公司提供的移动通讯服务的收费标准有两种套餐如表

    套餐

    套餐

    每月基本服务费（元）

    20

    30

    每月免费通话时间（分）

    100

    150

    每月超过免费通话时间加收通话费（元/分）

    0.4

    0.5

    李民选用了套餐

    （1）5月份李民的通话时间为120分钟，这个月李民应付话费多少元？

    （2）李民6月份的通话时间超过了150分钟，根据自己6月份的通话时间情况计算，如果自己选用套餐可以省4元钱，李民6月份的通话时间是多少分钟？

    （3）10月份李民改用了套餐，李民发现如果与9月份交相同的话费，10月份他可以多通话15分钟，李民9月份交了多少话费？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】你知道什么是“低碳生活”吗？“低碳生活”是指人们生活中尽量减少所耗能量，从而降低碳（特别是二氧化碳）的排放量的一种生活方式．

    （1）如果用x（L）表示耗油量，用y（kg）表示开私家车的二氧化碳排放量，则y与x之间的关系式可表示为___________；

    （2）在上述关系式中，耗油量每增加1L，二氧化碳排放量增加________kg．当耗油量从10L增加到100L时，二氧化碳排放量从________kg增加到________kg；

    （3）小颖家本月家居用电的耗电量约为90kwh、开私家车的耗油量约为70L、天然气使用量约20m、自来水使用量约6吨，请你计算一下小颖家本月这几项的二氧化碳排放总量；

    （4）你打算从哪些小事做起践行低碳生活？请直接写出两条．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】分如图，在ABCD中，点E、F分别是AD、BC的中点，分别连接BE、DF、BD．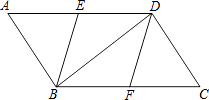

    （1）求证：△AEB≌△CFD；
    （2）若四边形EBFD是菱形，求∠ABD的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知∠MON = 50°，OE 平分∠MON，点A、B、C分别是射线OM、OE、ON上的动点(A、B、C不与点O重合)，连接AC交射线OE于点D、设∠OAC = x°．


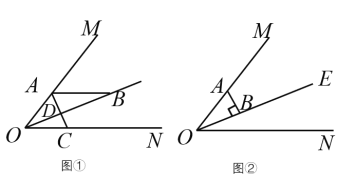
    （1）如图①，若AB//ON，

    ①则∠ABO 的度数是________；

    ②当∠BAD =∠ABD 时，x=_______；当∠BAD = ∠BDA 时，x=________．

    （2）如图②，若AB⊥OE，则是否存在这样的x值，使得 △ABD 中有一个角是另一个角的两倍．存在，直接写出x的值；不存在，说明理由．

    查看答案和解析>>

    同步练习册答案