
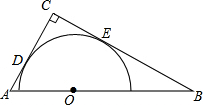
 如图,Rt△ABC中,∠ACB=90°,AC=4,BC=6,以斜边AB上的一点O为圆心所作的半圆分别与AC、BC相切于点D、E,则CD为
如图,Rt△ABC中,∠ACB=90°,AC=4,BC=6,以斜边AB上的一点O为圆心所作的半圆分别与AC、BC相切于点D、E,则CD为 解:连接OD、OE,
解:连接OD、OE,| AD |
| AC |
| OD |
| BC |
| 4-x |
| 4 |
| x |
| 6 |


 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
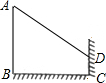 一位同学想利用树影测量树高,他在某一时间测得长为1m的竹竿影长0.8m,但当他马上测量树影时,因树靠近一幢建筑物,影子不完全落在地面上,有一部分影子在墙上,如图所示,他先测得留在墙上的影高为1.2m,又测得地面部分的影长为5m,测算一下这棵树的高时多少?
一位同学想利用树影测量树高,他在某一时间测得长为1m的竹竿影长0.8m,但当他马上测量树影时,因树靠近一幢建筑物,影子不完全落在地面上,有一部分影子在墙上,如图所示,他先测得留在墙上的影高为1.2m,又测得地面部分的影长为5m,测算一下这棵树的高时多少?查看答案和解析>>
科目:初中数学 来源: 题型:
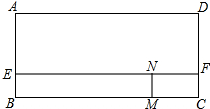 如图,已知矩形ABCD,AB=6cm,BC=8cm,E、F分别是AB、CD上的点,且AE=DF=4cm,两动点M、N分别从C、F两点同时出发沿CB、FE均以2cm/s的速度向B、E两点运动,猜测当M、N运动多长时间,矩形CFNM与矩形AEFD相似?写出你的猜测过程,与同学交流.
如图,已知矩形ABCD,AB=6cm,BC=8cm,E、F分别是AB、CD上的点,且AE=DF=4cm,两动点M、N分别从C、F两点同时出发沿CB、FE均以2cm/s的速度向B、E两点运动,猜测当M、N运动多长时间,矩形CFNM与矩形AEFD相似?写出你的猜测过程,与同学交流.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,点P在边AB上,点Q在边BC上,且BQ=x,AP=2x(0<x<5),连接PQ.
如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,点P在边AB上,点Q在边BC上,且BQ=x,AP=2x(0<x<5),连接PQ.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| a |
| 1 |
| a |
| 1 |
| a2 |
| 1 |
| a4 |
| 1 |
| a |
| a2+5a+1 |
| a2-2a+1 |
| a2 |
| a4+1 |
| a2 |
| a4+a2+1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com