
【题目】如图所示,一次函数y1=x+1的图象与x轴交于点A,与反比例函数![]() 的图象在第一象限内交于点B,作BC⊥x轴,垂足为C,且OC=1.
的图象在第一象限内交于点B,作BC⊥x轴,垂足为C,且OC=1.
(1)请直接写出在第一象限内,当x取何值时,y1>y2?
(2)将线段BC沿一次函数的图象平移至点B与点A重合,平移后点C的对应点是否在反比例函数的图象上?

【答案】(1)x>1;(2)在
【解析】(1)根据图象可知,在点B的右侧,一次函数的图象y1=x+1在反比例函数图象![]() 的上方,且点B的横坐标为1,可知当x>1时,y1>y2;(2)把x=1代入y1=x+1求出B点坐标(1,2),用待定系数法求出反比例函数解析式,之后用一次函数求出A点坐标(-1,0),根据BC的长是2,判断点(-1,-2)是否在反比例函数图象上即可得出结论.
的上方,且点B的横坐标为1,可知当x>1时,y1>y2;(2)把x=1代入y1=x+1求出B点坐标(1,2),用待定系数法求出反比例函数解析式,之后用一次函数求出A点坐标(-1,0),根据BC的长是2,判断点(-1,-2)是否在反比例函数图象上即可得出结论.
解:(1)当x>1时,y1>y2
(2)∵BC⊥x轴,垂足为C,且OC=1
∴C(1,0),点B的横坐标为1
当x=1时,y1=x+1=2,∴B(1,2)
∵点B在反比例函数的图象上
∴![]() ,∴k=2
,∴k=2
由y1=x+1=0,解得x=-1,∴A(-1,0)
∴将线段BC沿一次函数的图象平移至点B与点A重合时,线段BC向下平移了2个单位,向左平移了2个单位,平移后点C的对应点的坐标为(-1,-2)
当x=-1时, ![]()
∴平移后点C的对应点在反比例函数的图象上


 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,CD=6,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连结AG、CF. 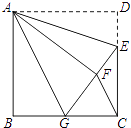
(1)求证:①△ABG≌△AFG; ②求GC的长;
(2)求△FGC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,把矩形OCBA放置于直角坐标系中,OC=3,BC=2,取AB的中点M,连结MC,把△MBC沿x轴的负方向平移OC的长度后得到△DAO.

(1)直接写出点D的坐标;
(2)已知点B与点D在经过原点的抛物线上,点P在第一象限内的该抛物线上移动,过点P作PQ⊥x轴于点Q,连结OP.
①若以O、P、Q为顶点的三角形与△DAO相似,试求出点P的坐标;
②试问在抛物线的对称轴上是否存在一点T,使得![]() 的值最大.若存在,求出T点坐标;若不存在,请说明理由.
的值最大.若存在,求出T点坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校计划购进一批电脑和电子白板,经过市场考察得知,购买1台电脑和2台电子白板需要3.5万元,购买2台电脑和1台电子白板需要2.5万元.
(1)求每台电脑,每台电子白板各多少万元?
(2)根据学校实际,需至少购进电脑和电子白板共30台,总费用不超过28万元,那么电子白板最多能买几台?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com