
分析 先将原代数式化简,根据分式的分母不能为0找出a的取值范围,再由a是方程x2+4x=0的根找出a的值,将a的值代入化简后的代数式即可得出结论.
解答 解:原式=[$\frac{(a+2)(a-2)}{(a-2)^{2}}$-$\frac{2}{a-2}$]×$\frac{a-2}{a(a+2)}$,
=($\frac{a+2}{a-2}$-$\frac{2}{a-2}$)×$\frac{a-2}{a(a+2)}$,
=$\frac{a}{a-2}$×$\frac{a-2}{a(a+2)}$,
=$\frac{1}{a+2}$.
∵a(a+2)(a-2)≠0,
∴a≠0且a≠±2.
∵a是方程x2+4x=x(x+4)=0的根,
∴a=0(舍去),或a=-4.
当a=-4时,原式=$\frac{1}{a+2}$=-$\frac{1}{2}$.
点评 本题考查了分式的化简求值和解一元二次方程中的因式分解法求值,解题的关键是:将原式化简并由分母不为0得出a的取值范围.本题属于基础题,解决此类题型时尤其要注意分母不能为0.


 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:初中数学 来源: 题型:选择题
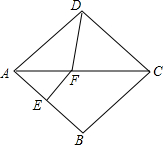 如图所示,在菱形ABCD中,∠BAD=70°,AB的垂直平分线交对角线AC于点F,垂足为E,连接DF,则∠CDF等于( )
如图所示,在菱形ABCD中,∠BAD=70°,AB的垂直平分线交对角线AC于点F,垂足为E,连接DF,则∠CDF等于( )| A. | 75° | B. | 70° | C. | 60° | D. | 55° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2$\sqrt{2}$ | C. | $\sqrt{2}$ | D. | $\frac{{\sqrt{2}}}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com