
【题目】已知二次函数![]() 的图象经过点
的图象经过点![]() .
.
(1)当![]() 时,若点
时,若点![]() 在该二次函数的图象上,求该二次函数的表达式;
在该二次函数的图象上,求该二次函数的表达式;
(2)已知点![]() ,
,![]() 在该二次函数的图象上,求
在该二次函数的图象上,求![]() 的取值范围;
的取值范围;
(3)当![]() 时,若该二次函数的图象与直线
时,若该二次函数的图象与直线![]() 交于点
交于点![]() ,
,![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 或2.
或2.
【解析】
(1)将![]() 和点
和点![]() ,
,![]() 代入解析式中,即可求出该二次函数的表达式;
代入解析式中,即可求出该二次函数的表达式;
(2)根据点M和点N的坐标即可求出该抛物线的对称轴,再根据二次函数的开口方向和二次函数的增加性,即可列出关于t的不等式,从而求出![]() 的取值范围;
的取值范围;
(3)将![]() 和点
和点![]() 代入解析式中,可得
代入解析式中,可得![]() ,然后将二次函数的解析式和一次函数的解析式联立,即可求出点P、Q的坐标,最后利用平面直角坐标系中任意两点之间的距离公式即可求出
,然后将二次函数的解析式和一次函数的解析式联立,即可求出点P、Q的坐标,最后利用平面直角坐标系中任意两点之间的距离公式即可求出![]() 的值.
的值.
解:(1)∵![]() ,
,
∴二次函数的表达式为![]() .
.
∵点![]() ,
,![]() 在二次函数的图象上,
在二次函数的图象上,
∴![]() .
.
解得![]() .
.
∴该抛物线的函数表达式为![]() .
.
(2)∵点![]() ,
,![]() 在该二次函数的图象上,
在该二次函数的图象上,
∴该二次函数的对称轴是直线![]() .
.
∵抛物线![]() 开口向上,
开口向上,
![]() ,
,![]() ,
,![]() 在该二次函数图象上,且
在该二次函数图象上,且![]() ,
,
∴点![]() ,
,![]() 分别落在点
分别落在点![]() 的左侧和右侧,
的左侧和右侧,
∴![]() .
.
解得![]() 的取值范围是
的取值范围是![]() .
.
(3)当![]() 时,
时,![]() 的图象经过点
的图象经过点![]() ,
,
∴![]() ,即
,即![]() .
.
∴二次函数表达式为![]() .
.
根据二次函数的图象与直线![]() 交于点
交于点![]() ,
,
由![]() ,解得
,解得![]() ,
,![]() .
.
∴点![]() 的横坐标分别是1,
的横坐标分别是1,![]() .
.
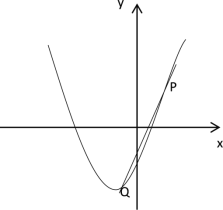
不妨设点![]() 的横坐标是1,则点
的横坐标是1,则点![]() 与点
与点![]() 重合,即
重合,即![]() 的坐标是
的坐标是![]() ,如下图所示
,如下图所示

∴点![]() 的坐标是
的坐标是![]() ,即
,即![]() 的坐标是
的坐标是![]() .
.
∵![]() ,
,
∴根据平面直角坐标系中任意两点之间的距离公式,可得![]() .
.
解得![]() 或2.
或2.


 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案科目:初中数学 来源: 题型:
【题目】科技发展,社会进步,中国已进入特色社会主义新时代,为实现“两个一百年”奋斗目标和中华民族伟大复兴的中国梦,需要人人奋斗,青少年时期是良好品格形成和知识积累的黄金时期,为此,大数据平台针对部分中学生品格表现和学习状况进行调查统计绘制如下统计图表,请根据图中提供的信息解决下列问题,类别:![]() 品格健全,成绩优异;
品格健全,成绩优异;![]() 尊敬师长,积极进取;
尊敬师长,积极进取;![]() 自控力差,被动学习;
自控力差,被动学习;![]() 沉迷奢玩,消极自卑.
沉迷奢玩,消极自卑.
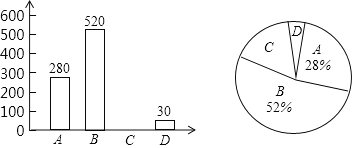
(1)本次调查被抽取的样本容量为 ;
(2)“自控力差,被动学习”的同学有 人,并补全条形统计图;
(3)样本中![]() 类所在扇形的圆心角为 度;
类所在扇形的圆心角为 度;
(4)东至县城内某中学有在校学生3330人,请估算该校![]() 类学生人数.
类学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,将
,将![]() 绕点
绕点![]() 旋转,它的两边分别交边
旋转,它的两边分别交边![]() 、
、![]() (或它们的延长线)于点
(或它们的延长线)于点![]() 、
、![]() .
.
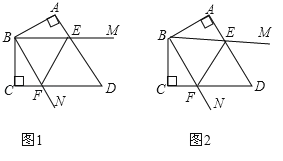
(1)当![]() 绕点
绕点![]() 旋转到
旋转到![]() 时(如图1),
时(如图1),
①求证:![]() ;
;
②求证:![]() ;
;
(2)当![]() 绕点
绕点![]() 旋转到如图2所示的位置时,
旋转到如图2所示的位置时,![]() ,此时,(1)中的两个结论是否还成立?请直接回答.
,此时,(1)中的两个结论是否还成立?请直接回答.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+bx+c的图象与x轴交于A(﹣4,0)和点B两点,与y轴交于点C,抛物线的对称轴是x=﹣1与x轴交于点D.
(1)求拋物线的函数表达式;
(2)若点P(m,n)为抛物线上一点,且﹣4<m<﹣1,过点P作PE∥x轴,交抛物线的对称轴x=﹣1于点E,作PF⊥x轴于点F,得到矩形PEDF,求矩形PEDF周长的最大值;
(3)点Q为抛物线对称轴x=﹣1上一点,是否存在点Q,使以点Q,B,C为顶点的三角形是直角三角形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《函数的图象与性质》拓展学习展示:
(问题)如图1,在平面直角坐标系中,抛物线G1:![]() 与x轴相交于A(-1,0),B(3,0)两点,与y轴交于点C,则a= ,b= .
与x轴相交于A(-1,0),B(3,0)两点,与y轴交于点C,则a= ,b= .
(操作)将图1中抛物线G1沿BC方向平移BC长度的距离得到抛物线G2,G2在y轴左侧的部分与G1在y轴右侧的部分组成的新图象记为G,如图②.请直接写出图象G对应的函数解析式.
(探究)在图2中,过点C作直线l平行于x轴,与图象G交于D,E两点.求图象G在直线l上方的部分对应的函数y随x的增大而增大时x的取值范围.
(应用)P是抛物线G2对称轴上一个动点,当△PDE是直角三角形时,直接写出P点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,AB=AC,AD是BC边上的中线,点E是AD上一点,过点B作BF∥EC,交AD的延长线于点F,连接BE,CF.
(1)求证:△BDF≌△CDE;
(2)当ED与BC满足什么数量关系时,四边形BECF是正方形?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
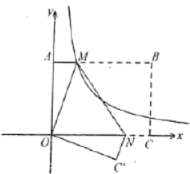
【题目】如图,在平面直角坐标系中,![]() 、
、![]() 分别为
分别为![]() 轴、
轴、![]() 轴正半轴上的点,以
轴正半轴上的点,以![]() 、
、![]() 为边,在一象限内作矩形
为边,在一象限内作矩形![]() ,且
,且![]() .将矩形
.将矩形![]() 翻折,使点
翻折,使点![]() 与原点重合,折痕为
与原点重合,折痕为![]() ,点
,点![]() 的对应点
的对应点![]() 落在第四象限,过
落在第四象限,过![]() 点的反比例函数
点的反比例函数![]()
![]() ,其图象恰好过
,其图象恰好过![]() 的中点,则点的
的中点,则点的![]() 坐标为________.
坐标为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系 xOy 中,菱形 ABOC 的顶点 O 在坐标原点,边 BO 在 x 轴的负半轴上,顶点 C的坐标为(﹣3,4),反比例函数 y ![]() 的图象与菱形对角线 AO 交于 D 点,连接 BD,当 BD⊥x 轴时,k的值是( )
的图象与菱形对角线 AO 交于 D 点,连接 BD,当 BD⊥x 轴时,k的值是( )

A.![]() B.
B.![]() C.﹣12D.
C.﹣12D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com