
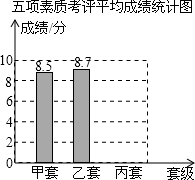
 我县某校通过初评决定最后从甲、乙、丙三个班中推荐一个班为校先进班集体,下表是这三个班的五项素质考核表:五项成绩素质考评得分表(单位:分)
我县某校通过初评决定最后从甲、乙、丙三个班中推荐一个班为校先进班集体,下表是这三个班的五项素质考核表:五项成绩素质考评得分表(单位:分)| 班级 | 行为规范 | 学习成绩 | 校运动会 | 艺术获奖 | 劳动卫生 |
| 甲 | 10 | 10 | 7 | 10 | 6 |
| 乙 | 10 | 8 | 8 | 9 | 8 |
| 丙 | 9 | 10 | 9 | 6 | 9 |
| 班级 | 平均数 | 众数 | 中位数 |
| 甲 | 8.6 | 10 | 10 |
| 乙 | 8.6 | 8 | 8 |
| 丙 | 8.6 | 9 | 9 |
分析 (1)根据平均数,中位数、众数,可得答案;
(2)根据中位数、众数,可得答案;
(3)根据加权平均数,可得答案.
解答 解(1)根据五项素质考核表可,得
五项成绩考评分析表(单位:分)
| 班级 | 平均数 | 众数 | 中位数 |
| 甲 | 8.6 | 10 | 10 |
| 乙 | 8.6 | 8 | 8 |
| 丙 | 8.6 | 9 | 9 |
点评 本题考查了条形统计图,观察统计图获得有效信息是解题关键,又利用了加权平均数、中位数、众数.


科目:初中数学 来源: 题型:选择题
| A. | 6 | B. | 24 | C. | 6或24 | D. | 6$\sqrt{5}$或$\sqrt{10}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{1±\sqrt{5}}{2}$ | D. | $\frac{1+\sqrt{5}}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
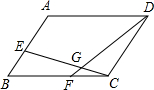 如图,若平行四边形ABCD的面积是1,E在AB上,F在BC上,且AE:EB=5:3,BF:FC=3:2,EC和FD相交于G,则△GFC的面积为$\frac{3}{115}$.
如图,若平行四边形ABCD的面积是1,E在AB上,F在BC上,且AE:EB=5:3,BF:FC=3:2,EC和FD相交于G,则△GFC的面积为$\frac{3}{115}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
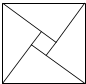 四个全等的直角三角形围成一个大正方形,中间空出的部分是一个小正方形,这样就组成了一个“赵爽弦图”(如图).如果小正方形面积为1,大正方形面积为13,直角三角形的两条直角边为a、b,那么(a+b)2的值是25.
四个全等的直角三角形围成一个大正方形,中间空出的部分是一个小正方形,这样就组成了一个“赵爽弦图”(如图).如果小正方形面积为1,大正方形面积为13,直角三角形的两条直角边为a、b,那么(a+b)2的值是25.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
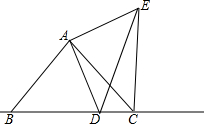 如图,△ABC为等腰直角三角形,AB=AC,∠BAC=90°
如图,△ABC为等腰直角三角形,AB=AC,∠BAC=90°查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
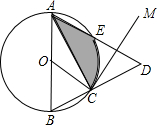 如图,AB是⊙O的直径,点C在⊙O上,以C为顶点在△ABC外侧作∠ACM=∠ABC.
如图,AB是⊙O的直径,点C在⊙O上,以C为顶点在△ABC外侧作∠ACM=∠ABC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com