
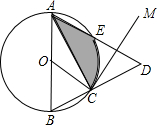
 如图,AB是⊙O的直径,点C在⊙O上,以C为顶点在△ABC外侧作∠ACM=∠ABC.
如图,AB是⊙O的直径,点C在⊙O上,以C为顶点在△ABC外侧作∠ACM=∠ABC.分析 (1)由AB为直径得到∠OCB+∠ACO=90°,加上∠B=∠OCB,∠B=∠ACM,则∠ACO+∠ACM=90°,所以OC⊥CM,于是根据切线的判定定理即可得到CM为⊙O的切线;
(2)在Rt△ACB=90°利用含30度的直角三角形三边的关系得到BC=$\frac{1}{2}$AB=3,AC=$\sqrt{3}$BC=3$\sqrt{3}$,由OA=OC得到S△AOC=S△BOC,则可计算出S△AOC=$\frac{1}{2}$S△ABC=$\frac{9}{4}$,然后根据扇形面积公式和阴影部分的面积=S扇形EOC进行计算.
解答 解:(1)CM与⊙O相切.理由如下:
∵AB为直径,
∴∠ACB=90°,即∠OCB+∠ACO=90°,
∵OB=OC,
∴∠B=∠OCB,
而∠B=∠ACM,
∴∠ACO+∠ACM=90°,即∠OCM=90°,
∴OC⊥CM,
∴CM为⊙O的切线;
(2)∵∠ACB=90°,∠ABC=60°,
∴∠BAC=30°,
∴BC=$\frac{1}{2}$AB=3,AC=$\sqrt{3}$BC=3$\sqrt{3}$,
∵OA=OC,
∴∠OAC=∠OCA=30°,S△AOC=S△BOC,
∴S△AOC=$\frac{1}{2}$S△ABC=$\frac{1}{2}$×$\frac{1}{2}$×$\sqrt{3}$×3$\sqrt{3}$=$\frac{9}{4}$,
∴阴影部分的面积=S扇形EOC
=$\frac{60•π•{3}^{2}}{360}$$\frac{120•π•{3}^{2}}{360}$-$\frac{9}{4}$
=$\frac{3}{2}$π.
故答案为$\frac{3}{2}$π.
点评 本切线的判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.也考查了扇形的计算.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
 我县某校通过初评决定最后从甲、乙、丙三个班中推荐一个班为校先进班集体,下表是这三个班的五项素质考核表:五项成绩素质考评得分表(单位:分)
我县某校通过初评决定最后从甲、乙、丙三个班中推荐一个班为校先进班集体,下表是这三个班的五项素质考核表:五项成绩素质考评得分表(单位:分)| 班级 | 行为规范 | 学习成绩 | 校运动会 | 艺术获奖 | 劳动卫生 |
| 甲 | 10 | 10 | 7 | 10 | 6 |
| 乙 | 10 | 8 | 8 | 9 | 8 |
| 丙 | 9 | 10 | 9 | 6 | 9 |
| 班级 | 平均数 | 众数 | 中位数 |
| 甲 | 8.6 | 10 | 10 |
| 乙 | 8.6 | 8 | 8 |
| 丙 | 8.6 | 9 | 9 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{6}{5}$ | B. | ?-$\frac{6}{5}$ | C. | $\frac{4}{5}$ | D. | ?-$\frac{4}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-a2)2=-a4 | B. | $\sqrt{3}$+$\sqrt{4}$=2$\sqrt{3}$ | C. | (π-2)0=0 | D. | ($\frac{1}{3}$)-2=9 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 由①式得x=$\frac{7}{3}$+4y,再代入②式 | B. | 由②式得y=$\frac{25+10x}{10}$,再代入①式 | ||
| C. | ①×3得③式,再将③式与②式相减 | D. | 由②式得9x=10y-25,再代入①式 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com