Question

6．引理：如图1所示已知Rt△ABC中，CD是斜边AB上的中线，则CD=AD=DB=$\frac{1}{2}$AB
应用格式为：∵CD是斜边AB上的中线，∴CD=AD=DB=$\frac{1}{2}$AB
如图2所示已知，△ABC中，AC=BC，∠ACB=90°，D为AB的中点，若E在直线AC上任意一点，DF⊥DE，交直线BC于F点．G为EF的中点，延长CG交AB直线于点H．
（1）若E在边AC上．①试说明DE=DF；②试说明CG=GH；（本题需要用引理）
（2）若AE=3，CH=5．求边AC的长．

Answer 1

分析 （1）①连接CD，推出CD=AD，∠CDF=∠ADE，∠A=∠DCB，证△ADE≌△CDF即可；
②连接DG，根据直角三角形斜边上中线求出CG=EG=GF=DG，推出∠GCD=∠GDC，推出∠GDH=∠GHD，推出DG=GH即可；
（2）由于E是直线AC上任意一点，所以分两种情况进行讨论：①E在线段AC上；②E在线段CA延长线上．求出EF=5，根据勾股定理求出EC；③E在AC延长线上时；即可得出答案．

解答 解：（1）①连接CD，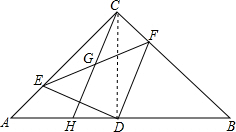
∵∠ACB=90°，D为AB的中点，AC=BC，
∴CD=AD=BD，
又∵AC=BC，
∴CD⊥AB，
∴∠EDA+∠EDC=90°，∠DCF=∠DAE=45°，
∵DF⊥DE，
∴∠EDF=∠EDC+∠CDF=90°，
∴∠ADE=∠CDF，
在△ADE和△CDF中，
$\left\{\begin{array}{l}{∠A=∠DCF}\\{AD=CD}\\{∠ADE=∠CDF}\end{array}\right.$，
∴△ADE≌△CDF，
∴DE=DF．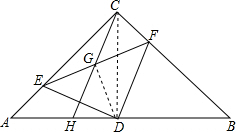
②连接DG，
∵∠ACB=90°，G为EF的中点，
∴CG=EG=FG，
∵∠EDF=90°，G为EF的中点，
∴DG=EG=FG，
∴CG=DG，
∴∠GCD=∠CDG
又∵CD⊥AB，
∴∠CDH=90°，
∴∠GHD+∠GCD=90°，∠HDG+∠GDC=90°，
∴∠GHD=∠HDG，
∴GH=GD，
∴CG=GH．

（2）分两种情况：
①如图，当E在线段AC上时，
∵CG=GH=EG=GF，
∴CH=EF=5，
∵△ADE≌△CDF，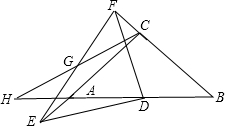
∴AE=CF=3，
∴在Rt△ECF中，由勾股定理得：CE=$\sqrt{E{F}^{2}-C{F}^{2}}$=4，
∴AC=AE+EC=3+4=7；
②如图，当E在线段CA延长线上时，
AC=EC-AE=4-3=1．
③E在AC延长线上时，AC=AE-CE，AC=3-4=-1（舍去）．
综合上述，AC=7或1．

点评 本题考查了直角三角形斜边上的中线，全等三角形的性质和判定的应用，主要考查学生综合运用定理进行推理的能力，有一定的难度．