
 已知△ABC中,AB=AC,∠ABC=60°,P是AC上一点,D是BC延长线上一点,且PB=PD,过D点作DE⊥AC,交AC延长线于点E,求AP与CE之间的数量关系.
已知△ABC中,AB=AC,∠ABC=60°,P是AC上一点,D是BC延长线上一点,且PB=PD,过D点作DE⊥AC,交AC延长线于点E,求AP与CE之间的数量关系.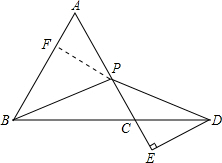 解:过P点作PF⊥AB于F,
解:过P点作PF⊥AB于F,
|
|


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com