
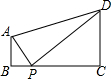
 如图,AB⊥BC,DC⊥BC,AB=1,DC=2,BC=3,点P是线段BC上一动点(不与点B、C重合),若△APD是等腰三角形,则CP的长是1或$\sqrt{6}$.
如图,AB⊥BC,DC⊥BC,AB=1,DC=2,BC=3,点P是线段BC上一动点(不与点B、C重合),若△APD是等腰三角形,则CP的长是1或$\sqrt{6}$. 分析 过A作AM⊥CD于M,根据勾股定理求出AD,分为三种情况:AD=DP或AD=AP或AP=DP,根据勾股定理求出CP,再逐个判断即可.
解答 解:如图: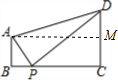
过A作AM⊥CD于M,
∵AB⊥BC,DC⊥BC,
∴∠AMD=90°,∠B=∠C=∠AMC=90°,
∴四边形ABCM是矩形,
∴CM=AB=1,AM=BC=3,
∴DM=2-1=1,
由勾股定理得:AD=$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$,
∵△APD是等腰三角形,
∴分为三种情况:
①AP=DP,设CP=x,则BP=3-x,
在Rt△ABP和Rt△DCP中,由勾股定理得:AB2+BP2=CP2+DC2,
即12+(3-x)2=x2+22,
解得:x=1,
CP=1;
②AD=DP=$\sqrt{10}$,
CP=$\sqrt{D{P}^{2}-D{C}^{2}}$=$\sqrt{(\sqrt{10})^{2}-{2}^{2}}$=$\sqrt{6}$;
③AD=AP=$\sqrt{10}$,
BP=$\sqrt{A{P}^{2}-B{P}^{2}}$=$\sqrt{(\sqrt{10})^{2}-{1}^{2}}$=3,
CP=3-3=0,此时P和C重合,不符合题意舍去;
故答案为:1或$\sqrt{6}$.
点评 本题考查了勾股定理,等腰三角形的性质的应用,能求出符合条件的所有情况是解此题的关键,用了分类讨论思想.


 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案科目:初中数学 来源: 题型:选择题
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,直线y=x+1分别与x轴、y轴相交于点A,B,以点A为圆心,AB长为半径画弧交x轴于点A1,再过点A1作x轴的垂线交直线于点B1,以点A为圆心,AB1长为半径画弧交x轴于点A2,…,按此做法进行下去,则点B4的坐标是( )
如图,直线y=x+1分别与x轴、y轴相交于点A,B,以点A为圆心,AB长为半径画弧交x轴于点A1,再过点A1作x轴的垂线交直线于点B1,以点A为圆心,AB1长为半径画弧交x轴于点A2,…,按此做法进行下去,则点B4的坐标是( )| A. | (2$\sqrt{2}$,2$\sqrt{2}$) | B. | (3,4) | C. | (4,4) | D. | (4$\sqrt{2}$-1,4$\sqrt{2}$) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
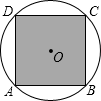 如图,正方形ABCD内接于⊙O,⊙O的直径为$\sqrt{2}$分米,若在这个圆面上随意抛一粒豆子,则豆子落在正方形ABCD内的概率是( )
如图,正方形ABCD内接于⊙O,⊙O的直径为$\sqrt{2}$分米,若在这个圆面上随意抛一粒豆子,则豆子落在正方形ABCD内的概率是( )| A. | $\frac{2}{π}$ | B. | $\frac{π}{2}$ | C. | $\frac{1}{2π}$ | D. | $\sqrt{2}π$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com