
 如图,圆柱形容器高为12cm,底面周长为10cm.在容器内壁距离容器底部3cm的点B处有一蚊子,此时一只壁虎正好在容器外壁,距离容器上沿3cm与蚊子相对的点A处,则壁虎捕捉蚊子需爬行的最短距离为13cm(不计壁厚).
如图,圆柱形容器高为12cm,底面周长为10cm.在容器内壁距离容器底部3cm的点B处有一蚊子,此时一只壁虎正好在容器外壁,距离容器上沿3cm与蚊子相对的点A处,则壁虎捕捉蚊子需爬行的最短距离为13cm(不计壁厚). 分析 将容器侧面展开,建立A关于EF的对称点A′,根据两点之间线段最短可知A′B的长度即为所求.
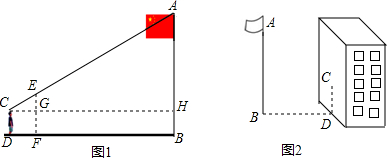
解答  解:如图:∵高为12cm,底面周长为10cm,在容器内壁离容器底部3cm的点B处有一蚊子,
解:如图:∵高为12cm,底面周长为10cm,在容器内壁离容器底部3cm的点B处有一蚊子,
此时一只壁虎正好在容器外壁,离容器上沿3cm与蚊子相对的点A处,
∴A′D=5cm,BD=12cm,
∴将容器侧面展开,作A关于EF的对称点A′,
连接A′B,则A′B即为最短距离,
A′B=$\sqrt{A′{D}^{2}+B{D}^{2}}$=$\sqrt{{5}^{2}+1{2}^{2}}$=13(Cm).
故壁虎捕捉蚊子的最短距离为13Cm.
故答案为:13.
点评 本题考查了平面展开-最短路径问题,将图形展开,利用轴对称的性质和勾股定理进行计算是解题的关键.同时也考查了同学们的创造性思维能力.


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:初中数学 来源: 题型:解答题
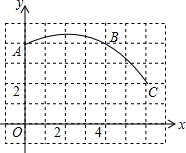 如图,在单位长度为1的正方形网格中建立一直角坐标系,一条圆弧经过网格点A、B、C,请在网格图中进行下列操作:
如图,在单位长度为1的正方形网格中建立一直角坐标系,一条圆弧经过网格点A、B、C,请在网格图中进行下列操作:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 数学活动课上,同学们围绕作图问题:“如图,已知直线l和l外一点P,用直尺和圆规作直线PQ,使PQ⊥l于点Q.”其中一位同学作出了如图所示的图形.你认为他的作法的理由有到线段两端点距离相等的点在这条线段的垂直平分线上;两点确定一条直线.
数学活动课上,同学们围绕作图问题:“如图,已知直线l和l外一点P,用直尺和圆规作直线PQ,使PQ⊥l于点Q.”其中一位同学作出了如图所示的图形.你认为他的作法的理由有到线段两端点距离相等的点在这条线段的垂直平分线上;两点确定一条直线.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com