
 为了给草坪喷水,安装了自动旋转喷水器,如图所示.设直线AD所在位置为地平面,喷水管AB高出地平面1.5m,在B处有一个自动旋转的喷水头,一瞬间喷出的水流呈抛物线状.喷头B与水流最高点C的连线与地平面成45°的角,水流的最高点C离地平面3.5m,水流的落地点为D.在建立如图所示的直角坐标系中:
为了给草坪喷水,安装了自动旋转喷水器,如图所示.设直线AD所在位置为地平面,喷水管AB高出地平面1.5m,在B处有一个自动旋转的喷水头,一瞬间喷出的水流呈抛物线状.喷头B与水流最高点C的连线与地平面成45°的角,水流的最高点C离地平面3.5m,水流的落地点为D.在建立如图所示的直角坐标系中:分析 (1)把抛物线的问题放到直角坐标系中解决,是探究实际问题常用的方法,本题关键是解等腰直角三角形,求出抛物线顶点C(2,3.5)及B(0,1.5),设顶点式求解析式;
(2)求AD,实际上是求当y=0时点D横坐标.
解答 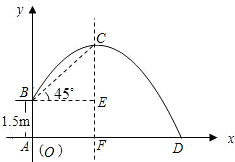 解:在如图所建立的直角坐标系中,
解:在如图所建立的直角坐标系中,
由题意知,B点的坐标为(0,1.5),∠CBE=45°,
∴△BEC为等腰直角三角形,
∴BE=2,
∴C点坐标为(2,3.5),
(1)设抛物线的函数解析式为
y=ax2+bx+c(a≠0),
则抛物线过点(0,1.5)顶点为(2,3.5),
∴当x=0时,y=c=1.5
由-$\frac{b}{2a}$,得b=-4a,
由$\frac{4ac-{b}^{2}}{4a}$,得$\frac{6a-16{a}^{2}}{4a}$,
解之,得a=0(舍去),a=-$\frac{1}{2}$,
∴b=-4a=2.
所以抛物线的解析式为y=-$\frac{1}{2}$x2+2x+$\frac{3}{2}$;
(2)∵D点为抛物线y=-$\frac{1}{2}$x2+2x+$\frac{3}{2}$的图象与x轴的交点,
∴当y=0时,即:-$\frac{1}{2}$x2+2x+$\frac{3}{2}$=0,
解得x=2±$\sqrt{7}$,
x=2-$\sqrt{7}$不合题意,舍去,取x=2+$\sqrt{7}$.
∴D点坐标为(2+$\sqrt{7}$,0),
∴AD=(2+$\sqrt{7}$)(m).
答:水流的落地点D到A点的距离是(2+$\sqrt{7}$)m.
点评 本题考查的是二次函数的应用,掌握待定系数法求函数解析式和二次函数的性质是解题的关键.


 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:初中数学 来源: 题型:解答题
 如图,AF是△ABC的高,点D、E分别在AB、AC上,且DE∥BC,DE交AF于点G.设AD=10,AB=30,AC=24,GF=12.
如图,AF是△ABC的高,点D、E分别在AB、AC上,且DE∥BC,DE交AF于点G.设AD=10,AB=30,AC=24,GF=12.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
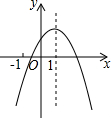 如图,二次函数y=ax2+bx+c的图象的对称轴是直线x=1,则下列结论:
如图,二次函数y=ax2+bx+c的图象的对称轴是直线x=1,则下列结论:| A. | 4个 | B. | 5个 | C. | 6个 | D. | 7个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1.62×104 | B. | 1.62×106 | C. | 1.62×108 | D. | 0.162×109 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,A点的坐标为(2,3),则tan∠AOy的值是( )
如图,A点的坐标为(2,3),则tan∠AOy的值是( )| A. | $\frac{2}{3}$ | B. | $\frac{3}{2}$ | C. | $\frac{{2\sqrt{13}}}{13}$ | D. | $\frac{{3\sqrt{13}}}{13}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 图象经过点(2,-1) | B. | 图象位于第二、四象限 | ||
| C. | 当x<0时,y随x的增大而减小 | D. | 当x>0时,y随x的增大而增大 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com