
【题目】阅读理解:
如图①,在正多边形![]() 的边
的边![]() 上任取一不与点
上任取一不与点![]() 重合的点
重合的点![]() ,并以线段
,并以线段![]() 为边在线段
为边在线段![]() 的上方作以正多边形
的上方作以正多边形![]() ,把正多边形
,把正多边形![]() 叫正多边形
叫正多边形![]() 的准位似图形,点
的准位似图形,点![]() 称为准位似中心.
称为准位似中心.
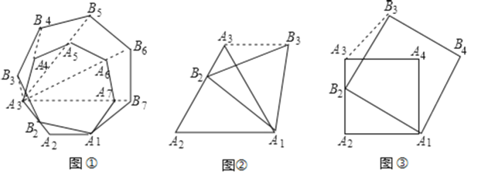
特例论证:
![]() 如图②已知正三角形
如图②已知正三角形![]() 的准位似图形为正三角形
的准位似图形为正三角形![]() ,试证明:随着点
,试证明:随着点![]() 的运动,
的运动,![]() 的大小始终不变.
的大小始终不变.
数学思考:
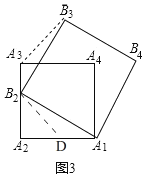
![]() 如图③已知正方形
如图③已知正方形![]() 的准位似图形为正方形
的准位似图形为正方形![]() ,随着点
,随着点![]() 的运动,
的运动,![]() 的大小始终不变?若不变,请求出
的大小始终不变?若不变,请求出![]() 的大小;若改变,请说明理由.
的大小;若改变,请说明理由.
归纳猜想:
![]() 在图①的情况下:
在图①的情况下:
①试猜想![]() 的大小是否会发生改变?若不改变,请用含n的代数式表示出
的大小是否会发生改变?若不改变,请用含n的代数式表示出![]() 的大小
的大小![]() 直接写出结果
直接写出结果![]() ;若改变,请说明理由.
;若改变,请说明理由.
②![]() ______
______![]() 用含n的代数式表示
用含n的代数式表示![]()
【答案】(1)证明详见解析;(2)![]() 的大小不变,证明详见解析;(3)①
的大小不变,证明详见解析;(3)①![]() 的大小始终不变,证明详见解析;②
的大小始终不变,证明详见解析;②![]()
【解析】
(1)先判断出△![]() △
△![]() ,再利用等边三角形的性质即可得出结论;
,再利用等边三角形的性质即可得出结论;
(2)先判断出△![]() △
△![]() ,再利用正方形的性质即可得出结论;
,再利用正方形的性质即可得出结论;
(3)①先判断出△![]() △
△![]() ,再利用正多边形的边相等和每个内角即可得出结论;
,再利用正多边形的边相等和每个内角即可得出结论;
②利用①的结论和方法即可得出结论.
![]() 证明:
证明:![]() 与
与![]() 是正三角形,
是正三角形,
![]() ,
,
![]() ,
,
![]() ≌
≌![]() ,
,
![]() ,
,
![]() 的大小不变;
的大小不变;
![]() 的大小不变,
的大小不变,
理由:如图,在边![]() 上取一点D,使
上取一点D,使![]() ,连接
,连接![]() ,
,
![]() 四边形
四边形![]() 与
与![]() 是正方形,
是正方形,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ≌
≌![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 是等腰直角三角形,
是等腰直角三角形,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
即:![]() 的大小始终不变;
的大小始终不变;
(3)①![]() 的大小始终不变,
的大小始终不变,
理由:如图1,
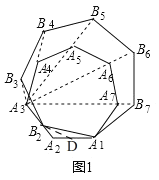
在![]() 上取一点D,使
上取一点D,使![]() ,
,
连接![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ≌
≌![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]() ;
;
②由①知,![]() ,
,
同①的方法可得,![]() ,
,
∴![]()
![]() ,
,
故答案为![]() .
.


 字词句段篇系列答案
字词句段篇系列答案科目:初中数学 来源: 题型:
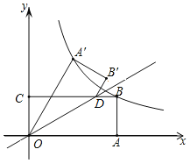
【题目】如图,矩形OABC的边OA,OC分别在x轴、y轴上,点B在第一象限,点D在边BC上,且∠AOD=30°,四边形OA′B′D与四边形OABD关于直线OD对称(点A′和A,B′和B分别对应).若AB=1,反比例函数y=![]() (k≠0)的图象恰好经过点A′,B,则k的值为______.
(k≠0)的图象恰好经过点A′,B,则k的值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年,某贫困户的家庭年人均纯收入为2500元,通过政府产业扶持,发展了养殖业后,到2018年,家庭年人均纯收入达到了3600元.
(1)求该贫困户2016年到2018年家庭年人均纯收入的年平均增长率;
(2)若年平均增长率保持不变,2019年该贫困户的家庭年人均纯收入是否能达到4200元?
查看答案和解析>>
科目:初中数学 来源: 题型:
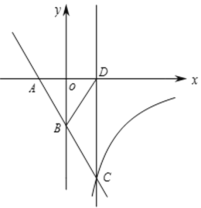
【题目】已知直线:y1=![]() 与x轴、y轴相交于A、B两点,与双曲线
与x轴、y轴相交于A、B两点,与双曲线![]() (k<0,x>0)相交于第四象限的点C,过点C作直线l⊥x轴,垂足为D,若△ABD的面积为
(k<0,x>0)相交于第四象限的点C,过点C作直线l⊥x轴,垂足为D,若△ABD的面积为![]() ,且B是AC的中点.
,且B是AC的中点.
(1)求k的值;
(2)直接写出![]() 的解集;
的解集;
(3)若P为直线l的一动点,点P的纵坐标为m,∠APB≥30°,求m的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中华文明,源远流长;中华汉字,寓意深广,为了传承优秀传统文化,某校团委组织了一次全校3000名学生参加的“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分.为了更好地了解本次大赛的成绩分布情况,随机抽取了其中200名学生的成绩(成绩x取整数,总分100分)作为样本进行整理,得到下列不完整的统计图表:
成绩x/分 | 频数 | 频率 |
50≤x<60 | 10 | 0.05 |
60≤x<70 | 30 | 0.15 |
70≤x<80 | 40 | n |
80≤x<90 | m | 0.35 |
90≤x≤100 | 50 | 0.25 |
请根据所给信息,解答下列问题:
(1)m= ,n= ;
(2)请补全频数分布直方图;
(3)若成绩在90分以上(包括90分)的为“优”等,则该校参加这次比赛的3000名学生中成绩“优”等约有多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)某商场销售一批名牌衬衫,平均每天可售出20件,每件盈利44元,为了扩大销售,增加盈利,尽快减少库存,商场决定采取适当的降价措施,经调查发现,如果每件衬衫每降价1元,商场平均每天可多售出5件.
(1)若商场平均每天要盈利1600元,每件衬衫应降价多少元?
(2)若该商场要每天盈利最大,每件衬衫应降价多少元?盈利最大是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A在反比例函数y=![]() (x>0)的图像上,点B在反比例函数y=
(x>0)的图像上,点B在反比例函数y=![]() (x>0)的图像上,AB∥x轴,BC⊥x轴,垂足为C,连接AC,若△ABC的面积是6,则k的值为( )
(x>0)的图像上,AB∥x轴,BC⊥x轴,垂足为C,连接AC,若△ABC的面积是6,则k的值为( )

A. 10 B. 12 C. 14 D. 16
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com