
【题目】已知抛物线C:y1=a(x﹣h)2﹣1,直线l:y2=kx﹣kh﹣1.
(1)求证:直线l恒过抛物线C的顶点;
(2)当a=﹣1,m≤x≤2时,y1≥x﹣3恒成立,求m的最小值;
(3)当0<a≤2,k>0时,若在直线l下方的抛物线C上至少存在两个横坐标为整数的点,求k的取值范围.
【答案】(1)见解析;(2)m的最小值为1;(3)k>4.
【解析】
(1)由抛物线的解析式可知抛物线的顶点坐标为(h,-1),然后证明点(h,-1)符合直线y2=kx﹣kh﹣1的解析式即可;
(2)令![]() ,依据拋物线的解析式可得到拋物线的顶点在直线y=-1上,由m≤x≤2时,y1≥x-3恒成立可得到拋物线的顶点坐标为(2,-1),然后找出抛物线y1=a(x﹣h)2﹣1位于直线
,依据拋物线的解析式可得到拋物线的顶点在直线y=-1上,由m≤x≤2时,y1≥x-3恒成立可得到拋物线的顶点坐标为(2,-1),然后找出抛物线y1=a(x﹣h)2﹣1位于直线![]() 上方时自变量x的取值范围,从而可确定出m的最小值;
上方时自变量x的取值范围,从而可确定出m的最小值;
(3)由(1)可知抛物线C与直线l都过点A(h,-1).当0<a≤3时,k>0,在直线l下方的抛物线C上至少存在两个横坐标为整数点,即当x=h+2时,![]() 恒成立,然后由
恒成立,然后由![]() 可得到关于k的不等式,从而可求得k:的取值范围.
可得到关于k的不等式,从而可求得k:的取值范围.
(1)抛物线C的顶点坐标为(h,﹣1),
当x=h时,y2=kh﹣kh﹣1=﹣1,
所以直线l恒过抛物线C的顶点;
(2)当a=﹣1时,抛物线C解析式为y1=﹣(x﹣h)2﹣1,
不妨令y3=x﹣3
如图1所示:抛物线C的顶点在直线y=﹣1上移动,
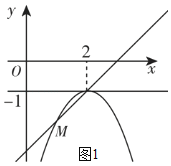
当m≤x≤2时,y1≥x﹣3恒成立,
则可知抛物线C的顶点为(2,﹣1),
设抛物线C与直线y3=x﹣3除顶点外的另一交点为M,
此时点M的横坐标即为m的最小值,
由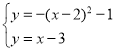 ,解得:x=1,x=2,
,解得:x=1,x=2,
所以m的最小值为1.
(3)如图2所示:由(1)可知:抛物线C与直线l都过点A(h,﹣1).
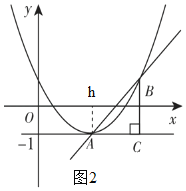
当0<a≤2时,k>0,在直线l下方的抛物线C上至少存在两个横坐标为整数点,即当x=h+2时,y2>y1恒成立.
所以k(h+2)﹣kh﹣1>a(h+2﹣h)2﹣1,整理得:k>2a.
又因为0<a≤2,
所以0<2a<4,所以k>4.


科目:初中数学 来源: 题型:
【题目】某学校为了解学生“第二课堂“活动的选修情况,对报名参加A.跆拳道,B.声乐,C.足球,D.古典舞这四项选修活动的学生(每人必选且只能选修一项)进行抽样调查.并根据收集的数据绘制了图①和图②两幅不完整的统计图.

根据图中提供的信息,解答下列问题:
(1)本次调查的学生共有 人;在扇形统计图中,B所对应的扇形的圆心角的度数是 ;
(2)将条形统计图补充完整;
(3)在被调查选修古典舞的学生中有4名团员,其中有1名男生和3名女生,学校想从这4人中任选2人进行古典舞表演.请用列表或画树状图的方法求被选中的2人恰好是1男1女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
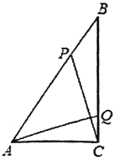
【题目】如图,![]() 中,
中,![]() ,
,![]() ,
,![]() ,动点
,动点![]() 从点
从点![]() 出发,在
出发,在![]() 边上以每秒
边上以每秒![]() 的速度向点
的速度向点![]() 匀速运动,同时动点
匀速运动,同时动点![]() 从点
从点![]() 出发,在
出发,在![]() 边上以每秒
边上以每秒![]() 的速度向点
的速度向点![]() 匀速运动,运动时间为
匀速运动,运动时间为![]() 秒(
秒(![]() ),连接
),连接![]() .
.
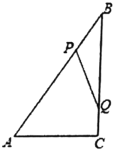
(1)若![]() 与
与![]() 相似,求
相似,求![]() 的值;
的值;
(2)连接![]() ,
,![]() ,若
,若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某篮球队对队员进行定点投篮测试,每人每天投篮10次,现对甲、乙两名队员在五天中进球数(单位:个)进行统计,结果如下:
甲 | 10 | 6 | 10 | 6 | 8 |
乙 | 7 | 9 | 7 | 8 | 9 |
经过计算,甲进球的平均数为8,方差为3.2.
(1)求乙进球的平均数和方差;
(2)如果综合考虑平均成绩和成绩稳定性两方面的因素,从甲、乙两名队员中选出一人去参加定点投篮比赛,应选谁?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
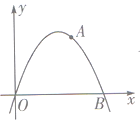
【题目】如图,抛物线![]() 交
交![]() 轴于
轴于![]() 、
、![]() 两点,
两点,![]() 为抛物线上一点,且横纵坐标相等(原点除外),
为抛物线上一点,且横纵坐标相等(原点除外),![]() 为抛物线上一动点,过
为抛物线上一动点,过![]() 作
作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,并与直线
,并与直线![]() 交于点
交于点![]() .
.
(1)求![]() 、
、![]() 两点的坐标.
两点的坐标.
(2)当点![]() 在线段
在线段![]() 上方时,过
上方时,过![]() 作
作![]() 轴的平行线与直线
轴的平行线与直线![]() 相交于点
相交于点![]() ,求
,求![]() 周长的最大值及此时
周长的最大值及此时![]() 点的坐标.
点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在△ABC中,AB=5cm,BC=7cm,S△ABC=14cm2,点P从点B出发,以3cm∕s的速度沿边BC向终点C运动,过点P作PQ⊥BC交折线BAC于点Q,D为PQ中点,以DQ为边向右侧作正方形DEFQ.设正方形DEFQ与△ABC重叠部分图形的面积是y(cm2),点P的运动时间为x(s).
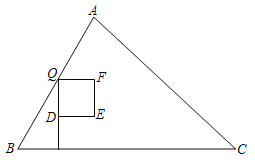
(1)∠C的度数为 ;
(2)当点P不与点C重合,且点F落在边AC上时x的值为 .
(3)当点P不与点B,C重合时,求y关于x的函数解析式;
(4)当直线BD平分△ABC的面积时,直接写出x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为推进素质教育,在初一年级设立了六个课外兴趣小组,如图是六个兴趣小组的频数分布直方图和扇形统计图,请根据图中提供的信息回答下列问题:
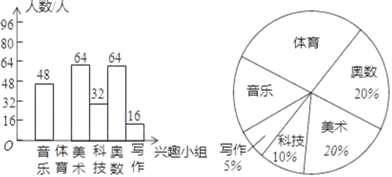
(1)初一年级共有多少人?
(2)补全频数分布直方图.
(3)求“从该年级中任选一名学生,是参加音乐、科技两个小组学生”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在不透明的袋中有大小、形状和质地等完全相同的4个小球,它们分别标有数字﹣1、﹣2、1、2.从袋中任意摸出一小球(不放回),将袋中的小球搅匀后,再从袋中摸出另一小球.
(1)请你用列表或画树状图的方法表示摸出小球上的数字可能出现的所有结果;
(2)将第一次摸出的数字作为点的横坐标x,第二次摸出的数字作为点的纵坐标y,求点(x,y)落在双曲线y=![]() 上的概率.
上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分10分)在某市组织的大型商业演出活动中,对团体购买门票实行优惠,决定在原定票价基础上每张降价80元,这样按原定票价需花费6000元购买的门票张数,现在只花费了4800元.
(1)求每张门票原定的票价;
(2)根据实际情况,活动组织单位决定对于个人购票也采取优惠措施,原定票价经过连续二次降价后降为324元,求平均每次降价的百分率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com